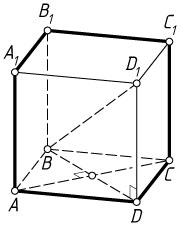
9605. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
все рёбра равны 6.
а) Докажите, что угол между прямыми AC
и BD_{1}
равен 90^{\circ}
.
б) Найдите расстояние между прямыми AC
и BD_{1}
.
Ответ. \sqrt{6}
.
Решение. а) Диагональ BD
квадрата ABCD
— ортогональная проекция наклонной D_{1}B
на плоскость ABCD
. Поскольку прямая AC
, лежащая в этой плоскости, перпендикулярна BD
(диагонали квадрата перпендикулярны), по теореме о трёх перпендикулярах наклонная D_{1}B
также перпендикулярна AC
.
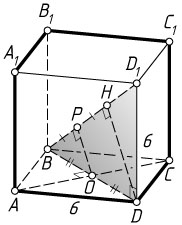
б) Опустим перпендикуляр OP
из центра O
квадрата ABCD
на диагональ BD_{1}
куба. Прямая OP
лежит в плоскости BDD_{1}
, перпендикулярной прямой AC
, значит, OP\perp AC
. Следовательно, OP
— общий перпендикуляр скрещивающихся прямых AC
и BD_{1}
. Его длина равна расстоянию между этими прямыми.
Пусть DH
— высота прямоугольного треугольника BDD_{1}
. Тогда
DH=\frac{DD_{1}\cdot BD}{BD_{1}}=\frac{6\cdot6\sqrt{2}}{6\sqrt{3}}=2\sqrt{6},
а так как OP
— средняя линия треугольника BDH
, то
OP=\frac{1}{2}DH=\sqrt{6}.
Источник: ЕГЭ. — 2018

