9606. На ребре AB
правильной четырёхугольной пирамиды SABCD
с основанием ABCD
отмечена точка Q
, причём AQ:BQ=1:2
. Точка P
— середина ребра AS
.
а) Докажите, что плоскость DPQ
перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ
, если площадь сечения DSB
равна 6.
Ответ. \sqrt{5}
.
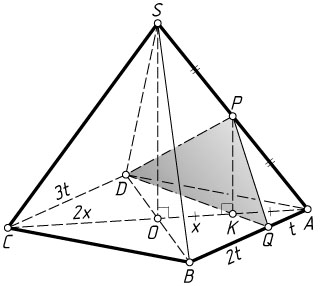
Решение. а) Пусть O
— центр квадрата ABCD
, K
— точка пересечения AC
и DQ
. Положим AQ=t
, BQ=2t
, AC=4x
. Тогда CD=AB=3t
и AO=2x
.
Треугольники AKQ
и CKD
подобны с коэффициентом \frac{AQ}{CD}=\frac{t}{3t}=\frac{1}{3}
, поэтому
AK=\frac{1}{3}CK=\frac{1}{3}\cdot3x=x=\frac{1}{2}AO.
Тогда PK
— средняя линия треугольника ASO
, значит, PK\parallel SO
, а так как пирамида правильная, то SO
— её высота. Следовательно, прямая PK
, параллельная SO
, также перпендикулярна плоскости основания пирамиды.
Плоскость DPQ
проходит через прямую PK
, перпендикулярную плоскости основания пирамиды, значит, по признаку перпендикулярности плоскостей, эти плоскости перпендикулярны.
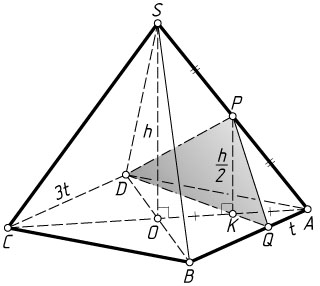
б) Пусть SO=h
. Тогда
6=S_{\triangle DSB}=\frac{1}{2}BD\cdot SO=\frac{1}{2}\cdot3t\sqrt{2}\cdot h=\frac{3th\sqrt{2}}{2},
откуда находим, что th=2\sqrt{2}
. Следовательно,
S_{\triangle DPQ}=\frac{1}{2}DQ\cdot PK=\frac{1}{2}\cdot\sqrt{t^{2}+9t^{2}}\cdot\frac{h}{2}=\frac{th\sqrt{10}}{4}=\frac{2\sqrt{2}\cdot\sqrt{10}}{4}=\sqrt{5}.
Источник: ЕГЭ. — 2018

