9620. Формула Крелле. Докажите, что для любого тетраэдра существует треугольник, длины сторон которого равны произведениям длин противоположных рёбер тетраэдра, причём площадь S
этого треугольника равна 6VR
, где V
— объём тетраэдра, R
— радиус его описанной сферы.
Решение. Пусть ABCD
— произвольный тетраэдр. Обозначим
DA=a,~DB=b,~DC=c,~BC=a',~AC=b',~AB=c'.
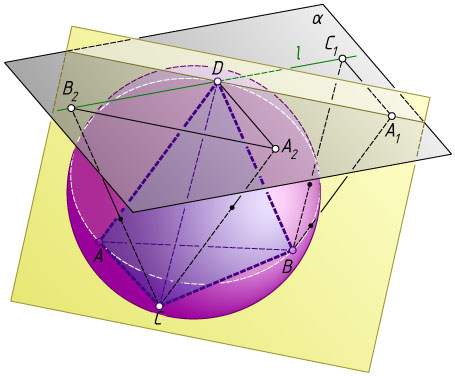
Через вершину D
проведём касательную плоскость \alpha
к описанной сфере тетраэдра. Пусть l
— прямая пересечения этой плоскости с плоскостью BDC
(рис. 1). Через точку B
проведём прямые параллельные DA
и DC
, пересекающие касательную плоскость в точках A_{1}
и C_{1}
соответственно. Через точку C
проведём прямые параллельные DA
и DB
, пересекающие касательную плоскость в точках A_{2}
и B_{2}
соответственно. Тогда прямые BC_{1}
и CB_{2}
лежат в плоскости BDC
, поэтому точки C_{1}
, B_{2}
и D
лежат на прямой l
.
Плоскости BA_{1}C_{1}
и ADC
параллельны, поэтому прямая A_{1}C_{1}
параллельна прямой пересечения касательной плоскости с плоскостью ADC
, т. е. прямой DA_{2}
. Аналогично B_{2}A_{2}\parallel DA_{1}
, значит, треугольники DA_{1}C_{1}
и B_{2}A_{2}D
подобны.
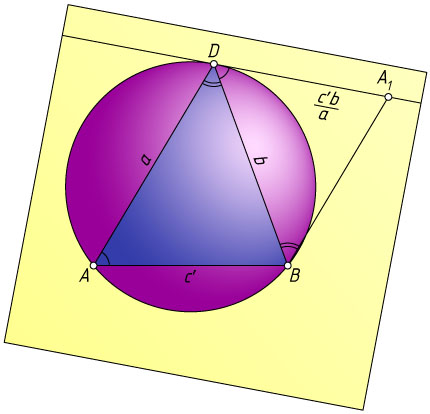
Рассмотрим сечение сферы плоскостью ABA_{1}D
(рис. 2). Получим окружность, описанную около треугольника ABD
, и касательную DA_{1}
к ней в точке D
. Из теоремы об угле между касательной и хордой, а также из параллельности прямых BA_{1}
и AD
следует, что
\angle BDA_{1}=\angle BAD~\mbox{и}~\angle DBA_{1}=\angle ADB.
Значит, треугольники DBA_{1}
и ADB
подобны, поэтому \frac{DA_{1}}{AB}=\frac{DB}{DA}
, откуда
DA_{1}=\frac{DB\cdot AB}{DA}=\frac{c'b}{a}.
Аналогично находим, что
DC_{1}=\frac{a'b}{c},~DA_{2}=\frac{b'c}{a},~DB_{2}=\frac{a'c}{b}.
Треугольники DA_{1}C_{1}
и B_{2}A_{2}D
подобны, поэтому \frac{A_{1}C_{1}}{DA_{2}}=\frac{DC_{1}}{DB_{2}}
, или \frac{A_{1}C_{1}}{\frac{b'c}{a}}=\frac{\frac{a'b}{c}}{\frac{a'c}{b}}
, откуда A_{1}C_{1}=\frac{b'b^{2}}{ac}
.
Таким образом, длины сторон треугольника A_{1}DC_{1}
равны \frac{c'b}{a}
, \frac{a'b}{c}
и \frac{b'b^{2}}{ac}
. Умножив их на \frac{ac}{b}
, получим числа cc'
, aa'
и bb'
, т. е. произведения длин противоположных рёбер тетраэдра. Следовательно, существует треугольник, длины сторон которого равны cc'
, aa'
, bb'
.
Тогда из подобия получаем, что
S_{1}=S_{\triangle DA_{1}C_{1}}=\frac{b^{2}}{a^{2}c^{2}}\cdot S.
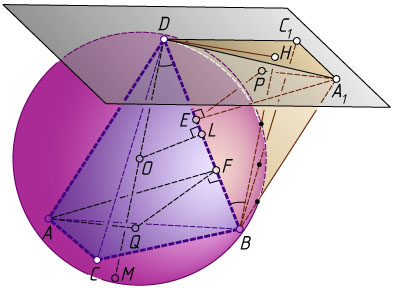
Вычислим теперь объём V_{1}
тетраэдра DA_{1}C_{1}B
. Пусть DM=2R
— диаметр описанной сферы тетраэдра ABCD
, а BH
— высота тетраэдра DA_{1}C_{1}B
. Тогда прямые BH
и DM
параллельны, так как они перпендикулярны одной и той же плоскости — касательной плоскости, проведённой в точке D
к описанной сфере тетраэдра ABCD
.
Опустим перпендикуляр OL
из центра O
этой сферы на ребро DB
. Прямоугольные треугольники BDH
и DOL
подобны, значит, \frac{BH}{BD}=\frac{DL}{OD}
, откуда
BH=\frac{BD\cdot DL}{OD}=\frac{b\cdot\frac{b}{2}}{R}=\frac{b^{2}}{2R},
поэтому
V_{1}=V_{DA_{1}C_{1}B}=\frac{1}{3}BH\cdot S_{1}=\frac{1}{3}\cdot\frac{b^{2}}{2R}\cdot\frac{b^{2}}{a^{2}c^{2}}\cdot S=\frac{b^{4}}{6Ra^{2}c^{2}}S.
Из подобия треугольников DBA_{1}
и ADB
следует, что \frac{S_{\triangle DBA_{1}}}{S_{\triangle ADB}}=\frac{b^{2}}{a^{2}}
, а из подобия треугольников BDC_{1}
и DCB
— \frac{S_{\triangle BDC_{1}}}{S_{\triangle DCB}}=\frac{b^{2}}{c^{2}}
.
Отношение объёмов тетраэдров DA_{1}C_{1}B
и ABCD
равно произведению отношения площадей их граней BC_{1}D
и BCD
и отношения высот A_{1}P
и AQ
, опущенных на эти грани. В свою очередь, отношение этих высот равно отношению высот A_{1}E
и AF
треугольников A_{1}BD
и ABD
, опущенных на их общую сторону BD
, т. е. отношению площадей этих треугольников. Тогда
\frac{V_{1}}{V}=\frac{S_{\triangle BC_{1}D}}{S_{\triangle BCD}}\cdot\frac{S_{\triangle DBA_{1}}}{S_{\triangle ADB}}=\frac{b^{2}}{c^{2}}\cdot\frac{b^{2}}{a^{2}}=\frac{b^{4}}{a^{2}c^{2}}.
Следовательно,
V=\frac{a^{2}c^{2}}{b^{4}}V_{1}=\frac{a^{2}c^{2}}{b^{4}}\cdot\frac{b^{4}}{6Ra^{2}c^{2}}S=\frac{S}{6R},
откуда S=6VR
.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 6.9, с. 101
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 8.12, с. 109
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 319, с. 42


