9719. Дана треугольная пирамида SABC
, в которой SA=BC=2\sqrt{5}
, AB=AC=\sqrt{29}
, SB=SC=\sqrt{13}
.
а) Докажите, что ребро SA
перпендикулярно ребру BC
.
б) Найдите угол между прямой SA
и плоскостью BSC
.
Ответ. \arccos\frac{1}{2\sqrt{10}}
.
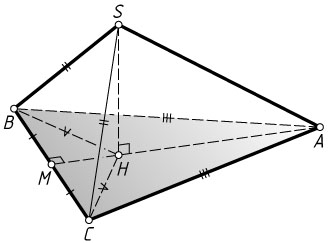
Решение. а) Пусть SH
— высота пирамиды. Наклонные SB
и SC
на плоскость ABC
равны, поэтому равны их ортогональные проекции на эту плоскость, т. е. HB=HC
. Точка H
равноудалена от концов основания BC
равнобедренного треугольника ABC
, поэтому она лежит на серединном перпендикуляре, а значит, на высоте AM
этого треугольника. Прямая AH
— ортогональная проекция наклонной SA
на плоскость ABC
. Следовательно, по теореме о трёх перпендикулярах SA\perp BC
.
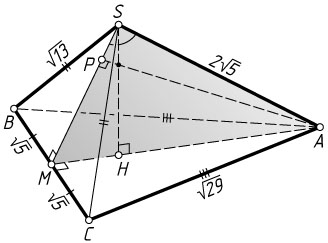
б) Пусть AP
— высота треугольника AMS
. Прямая BC
перпендикулярна плоскости SAM
, так как эта прямая перпендикулярна двум пересекающимся прямым SM
и AM
этой плоскости. Значит, AP\perp BC
. Таким образом, прямая AP
перпендикулярна двум пересекающимся прямым BC
и SM
плоскости BSC
. Следовательно, AP
— перпендикуляр к плоскости BSC
, а SC
— ортогональная проекция наклонной AS
на плоскость BSC
. Тогда угол между прямой SA
и плоскостью BSC
— это угол ASP
.
По теореме Пифагора
SM=\sqrt{SB^{2}-BM^{2}}=\sqrt{13-5}=\sqrt{8}=2\sqrt{2},
AM=\sqrt{AB^{2}-BM^{2}}=\sqrt{29-5}=\sqrt{24}=2\sqrt{6}.
По теореме косинусов
\cos\angle ASP=\cos\angle ASM=\frac{SM^{2}+SA^{2}-AM^{2}}{2SM\cdot SA}=\frac{8+20-24}{2\cdot2\sqrt{2}\cdot2\sqrt{5}}=\frac{1}{2\sqrt{10}}.
Источник: ЕГЭ. — 2019, 29 марта, досрочный экзамен, № 14

