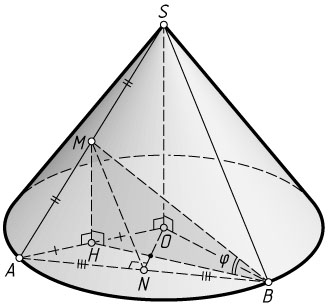
9728. Радиус основания конуса с вершиной S
и центром основания O
равен 5, а его высота равна \sqrt{51}
. Точка M
— середина образующей SA
конуса, а точки N
и B
лежат на основании конуса, причём прямая MN
параллельна образующей конуса SB
.
а) Докажите, что угол ANO
— прямой.
б) Найдите угол между прямой BM
и плоскостью основания конуса, если AB=8
.
Ответ. 30^{\circ}
.
Решение. а) Точка M
— середина образующей SA
, а MN\parallel SB
, поэтому N
— середина хорды AB
основания. Значит, ON
— медиана равнобедренного треугольника AOB
с основанием AB
. Следовательно, ON
— высота этого треугольника, т. е. \angle ANO=90^{\circ}
.
б) Пусть H
— середина отрезка OA
. Тогда MH
— средняя линия прямоугольного треугольника ASO
, а так как SO
— высота конуса и MH\parallel SO
, то MH
— перпендикуляр к плоскости основания конуса. Тогда BH
— ортогональная проекция наклонной MB
на плоскость основания, а MBH
— искомый угол. Обозначим \angle MBH=\varphi
.
По формуле для медианы
BH=\frac{1}{2}\sqrt{2AB^{2}+2OB^{2}-AO^{2}}=\frac{1}{2}\sqrt{2\cdot64+2\cdot25-25}=\frac{\sqrt{153}}{2}.
Значит,
\tg\varphi=\frac{MH}{BH}=\frac{\frac{\sqrt{51}}{2}}{\frac{\sqrt{153}}{2}}=\frac{1}{\sqrt{3}}.
Следовательно \varphi=30^{\circ}
.
Источник: ЕГЭ. — 2019, задача 14
