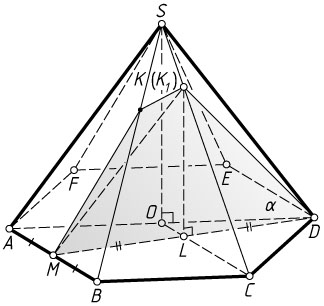
9759. В правильной шестиугольной пирамиде SABCDEF
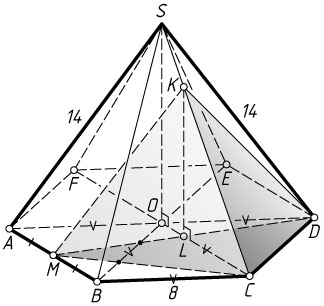
боковое ребро SA=14
, а сторона основания AB=8
. Точка M
— середина стороны AB
основания. Плоскость \alpha
проходит через точки M
и D
и перпендикулярна плоскости ABC
. Прямая SC
пересекает плоскость \alpha
в точке K
.
а) Докажите, что MK=KD
.
б) Найдите объём пирамиды MCDK
.
Ответ. 36\sqrt{11}
.
Решение. а) Пусть O
— центр основания ABCDEF
, L
— точка пересечения отрезков MD
и OC
. Точка O
— середина AD
, а OL\parallel AM
, значит, L
— середина MD
.
Пусть прямая, проведённая через точку L
параллельно SO
, пересекает ребро SC
в точке K_{1}
. Тогда K_{1}L
— перпендикуляр к плоскости основания пирамиды, поэтому по признаку перпендикулярности плоскостей плоскость MK_{1}D
перпендикулярна плоскости основания, а значит, совпадает с плоскостью \alpha
. Тогда точка K_{1}
совпадает с K
.
В треугольнике MKD
медиана KL
является высотой, следовательно, этот треугольник равнобедренный, и MK=KD
.
б) Большие диагонали разбивают правильный шестиугольник на шесть равных равносторонних треугольников, поэтому BC=OC=OA=OD=8
.
Отрезок OL
— средняя линия треугольника AMD
, поэтому
OL=\frac{1}{2}AM=\frac{1}{4}AB=2.
Тогда
CL=OC-OL=8-2=6,
значит, \frac{CL}{OC}=\frac{6}{8}=\frac{3}{4}
. Из подобия треугольников KLC
и SOC
находим, что
KL=SO\cdot\frac{CL}{OC}=\frac{3}{4}\sqrt{SA^{2}-OA^{2}}=\frac{3}{4}\sqrt{14^{2}-8^{2}}=\frac{3}{4}\cdot2\sqrt{33}=\frac{3\sqrt{33}}{2}.
Заметим, что
S_{\triangle CMD}=2S_{\triangle CDL}=2\cdot\frac{3}{4}S_{\triangle CDO}=\frac{3}{2}\cdot\frac{8^{2}\sqrt{3}}{4}=24\sqrt{3}.
Следовательно,
V_{MCDK}=\frac{1}{3}KL\cdot S_{\triangle CDM}=\frac{1}{3}\cdot\frac{3\sqrt{33}}{2}\cdot24\sqrt{3}=36\sqrt{11}.
Источник: ЕГЭ. — 2020, июль, задача 14

