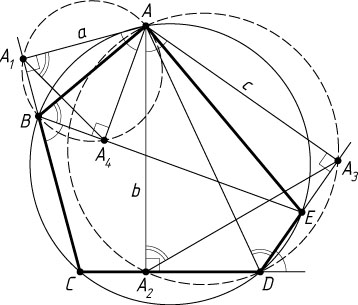
70. Пятиугольник ABCDE
вписан в окружность. Расстояния от точки A
до прямых BC
, DC
и DE
равны соответственно a
, b
и c
. Найдите расстояние от вершины A
до прямой BE
.
Ответ. \frac{ac}{b}
.
Указание. Пусть A_{1}
, A_{2}
, A_{3}
, A_{4}
— основания перпендикуляров, опущенных из точки A
на прямые BC
, CD
, DE
и BE
соответственно. Тогда треугольник AA_{1}A_{4}
подобен треугольнику AA_{2}A_{3}
.
Можно также воспользоваться результатом задачи 11251.
Решение. Первый способ. Пусть A_{1}
, A_{2}
, A_{3}
, A_{4}
— основания перпендикуляров, опущенных из точки A
на прямые BC
, DC
, DE
и BE
соответственно. Докажем, что треугольник AA_{1}A_{4}
подобен треугольнику AA_{2}A_{3}
.
Действительно,
\angle A_{1}AA_{4}=180^{\circ}-\angle A_{1}BA_{4}=\angle CBE=180^{\circ}-\angle CDE=\angle A_{2}AA_{3}.
Точки A_{1}
и A_{4}
лежат на окружности с диаметром AB
, а точки A_{2}
и A_{3}
— на окружности с диаметром AD
. Поэтому
\angle AA_{1}A_{4}=\angle ABE=\angle ADE=\angle AA_{2}A_{3}.
Из доказанного следует, что \frac{AA_{1}}{AA_{2}}=\frac{AA_{4}}{AA_{3}}
. Отсюда находим, что
AA_{4}=AA_{1}\cdot\frac{AA_{3}}{AA_{2}}=\frac{ac}{b}.
Второй способ. Пусть расстояние от вершины A
до прямой BE
равно x
. Для вписанного четырёхугольника BCDE
верно равенство ac=bx
(см. задачу 11251). Следовательно, x=\frac{ac}{b}
.