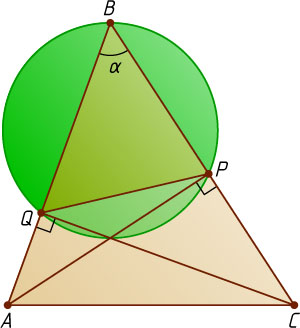
77. В остроугольном треугольнике ABC
из вершин A
и C
на стороны BC
и AB
опущены высоты AP
и CQ
. Найдите сторону AC
, если известно, что периметр треугольника ABC
равен 15, периметр треугольника BPQ
равен 9, а радиус окружности, описанной около треугольника BPQ
, равен \frac{9}{5}
.
Ответ. \frac{24}{5}
.
Решение. Обозначим \angle ABC=\alpha
. Треугольник PBQ
подобен треугольнику ABC
с коэффициентом \frac{BP}{AB}=\cos\alpha
(см. задачу 19), а так как отношение периметров подобных треугольников равно коэффициенту подобия, то \cos\alpha=\frac{9}{15}=\frac{3}{5}
, \sin\alpha=\frac{4}{5}
. Тогда, если r
и R
— радиусы описанных окружностей подобных треугольников PBQ
и ABC
, то
R=\frac{5}{3}r=\frac{5}{3}\cdot\frac{9}{5}=3.
Следовательно,
AC=2R\sin\alpha=2\cdot3\cdot\frac{4}{5}=\frac{24}{5}.