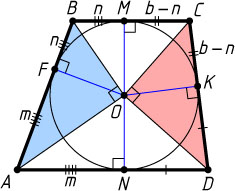
317. Окружность, вписанная в трапецию ABCD
, касается боковой стороны AB
в точке F
. Найдите площадь трапеции, если AF=m
, FB=n
, а меньшее основание трапеции BC
равно b
.
Ответ. \left(b+m+\frac{mn}{b-n}\right)\sqrt{mn}
.
Указание. Проведите радиус в точку касания со стороной AB
и примените теорему о высоте, опущенной из вершины прямого угла на гипотенузу.
Решение. Пусть O
— центр окружности; M
, K
, N
— точки касания со сторонами BC
, CD
, AD
соответственно, R
— радиус окружности. Тогда (см. задачу 656)
OF^{2}=BF\cdot AF=mn,~R=OF=\sqrt{mn},~CK=CM=CB-BM=b-n.
Поскольку OK^{2}=CK\cdot KD
, то
KD=\frac{mn}{b-n},~AD=AN+ND=m+\frac{mn}{b-n}.
Следовательно,
S_{ABCD}=\frac{BC+AD}{2}\cdot2R=\frac{1}{2}\left(b+m+\frac{mn}{b-n}\right)\cdot2\sqrt{mn}=\left(b+m+\frac{mn}{b-n}\right)\sqrt{mn}.