319. Около окружности радиуса \frac{2}{\sqrt{3}}
описана равнобедренная трапеция. Угол между диагоналями трапеции, опирающийся на основание, равен 2\arctg\frac{2}{\sqrt{3}}
. Найдите отрезок, соединяющий точки касания окружности с большим основанием трапеции и одной из её боковых сторон.
Ответ. 2.
Указание. Обозначьте половины оснований трапеции через x
и y
; найдите x
, y
и угол между боковой стороной и большим основанием.
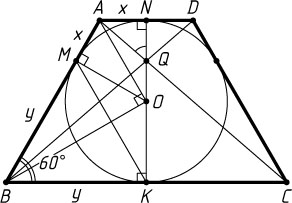
Решение. Пусть Q
— точка пересечения диагоналей AC
и BD
трапеции ABCD
; N
, M
и K
— точки касания вписанной окружности с меньшим основанием AD
, боковой стороной AB
и большим основанием BC
соответственно; O
— центр окружности. Обозначим AN=x
, BK=y
. Поскольку треугольник AOB
прямоугольный (см. задачу 313), а OM
— его высота, опущенная на гипотенузу,
\frac{4}{3}=OM^{2}=AM\cdot BM=AN\cdot BK=xy,
x+y=AN+BK=(NQ+QK)\tg\angle AQN=\frac{8}{3}.
Из полученной системы находим, что x=\frac{2}{3}
и y=2
. Следовательно,
\cos\angle ABK=\frac{y-x}{y+x}=\frac{1}{2},~\angle ABK=60^{\circ},~MK=y=2.