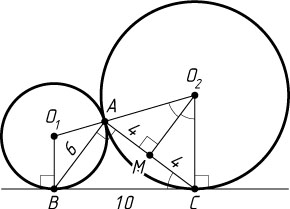
370. Две окружности касаются друг друга внешним образом в точке A
. Найдите радиусы окружностей, если хорды, соединяющие точку A
с точками касания с одной из общих внешних касательных, равны 6 и 8.
Ответ. \frac{15}{4}
; \frac{20}{3}
.
Указание. Опустите перпендикуляр из центра одной из окружностей на соответствующую хорду и рассмотрите получившиеся подобные треугольники.
Решение. Первый способ. Пусть O_{1}
и O_{2}
— центры окружностей, B
и C
— указанные точки касания (AB=6
, AC=8
). Поскольку треугольник BAC
прямоугольный с прямым углом при вершине A
(см. задачу 365), то BC=10
.
Пусть M
— основание перпендикуляра, опущенного из O_{2}
на AC
. Из подобия треугольников O_{2}MC
и CAB
находим, что
O_{2}C=BC\cdot\frac{CM}{AB}=10\cdot\frac{4}{6}=\frac{20}{3}.
Аналогично находим, что O_{1}B=\frac{15}{4}
.
Второй способ. Продолжим хорду AB
первой окружности до пересечения со второй в точке D
. Поскольку \angle CAD=\angle CAB=90^{\circ}
(см. задачу 365), отрезок CD
— диаметр второй окружности. Значит, CD\perp BC
. Отрезок AC=8
— высота прямоугольного треугольника BCD
, проведённая из вершины прямого угла, поэтому
AD=\frac{AC^{2}}{AB}=\frac{64}{6}=\frac{32}{3}.
Пусть R
— искомый радиус второй окружности. Тогда
4R^{2}=CD^{2}=BD\cdot AD=(AB+AD)AD=\left(6+\frac{32}{3}\right)\cdot\frac{32}{3}=\frac{50}{3}\cdot\frac{32}{3}=\frac{25\cdot64}{9},
откуда 2R=\frac{40}{3}
. Следовательно, R=\frac{20}{3}
. Аналогично находим, что радиус второй окружности равен \frac{15}{4}
.