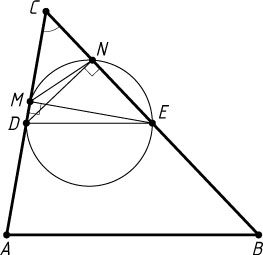
496. В треугольнике ABC
на средней линии DE
, параллельной AB
, как на диаметре построена окружность, пересекающая стороны AC
и BC
в точках M
и N
. Найдите MN
, если BC=a
, AC=b
, AB=c
.
Ответ. \frac{c(a^{2}+b^{2}-c^{2})}{4ab}
.
Указание. Треугольники CMN
и CED
подобны с коэффициентом |\cos\angle ACB|
(см. задачу 19).
Решение. Точки M
и N
лежат на окружности с диаметром DE
, поэтому DN
и EM
— высоты треугольника CDE
, значит, треугольники CMN
и CED
подобны с коэффициентом \cos\angle ACB
(см. задачу 19). Следовательно,
MN=DE\cos\angle ACB=\frac{c}{2}\cdot\frac{a^{2}+b^{2}-c^{2}}{2ab}=\frac{c(a^{2}+b^{2}-c^{2})}{4ab}.