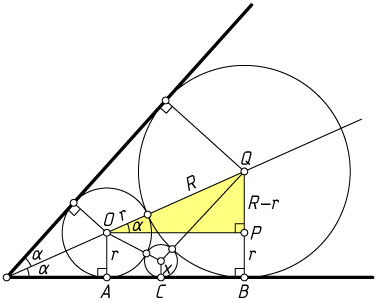
660. В угол величины 2\alpha
вписаны две касающиеся окружности. Найдите отношение радиуса меньшей окружности к радиусу третьей окружности, касающейся первых двух и одной из сторон угла.
Ответ. \frac{2(1+\cos\alpha)}{1+\sin\alpha}
.
Указание. Длина отрезка общей внешней касательной к двум касающимся окружностям радиусов r
и R
, заключённого между точками касания, равна 2\sqrt{rR}
.
Решение. Пусть r
и R
— радиусы данных окружностей (r\lt R
), O
и Q
соответственно — их центры, A
и B
соответственно — точки касания с одной из сторон угла, x
— радиус третьей окружности, C
— её точка касания с той же стороной угла.
Поскольку
AB=AC+BC,~AB=2\sqrt{rR},~AC=2\sqrt{rx},~BC=2\sqrt{Rx}
(см. задачу 365), то
2\sqrt{rx}+2\sqrt{Rx}=2\sqrt{rR}.
Из этого уравнения находим, что
x=\frac{rR}{(\sqrt{r}+\sqrt{R})^{2}}.
Тогда
\frac{r}{x}=\frac{(\sqrt{r}+\sqrt{R})^{2}}{R}=\left(\frac{\sqrt{r}+\sqrt{R}}{\sqrt{R}}\right)^{2}=\left(\sqrt{\frac{r}{R}}+1\right)^{2}.
Опустим из точки O
перпендикуляр OP
на радиус QB
. В прямоугольном треугольнике OPQ
OQ=r+R,~PQ=R-r,~\angle POQ=\alpha.
Поэтому
R-r=(R+r)\sin\alpha,~\mbox{или}~1-\frac{r}{R}=\left(1+\frac{r}{R}\right)\sin\alpha.
Отсюда находим, что
\frac{r}{R}=\frac{1-\sin\alpha}{1+\sin\alpha}=\frac{\cos^{2}\alpha}{(1+\sin\alpha)^{2}}.
Следовательно,
\frac{r}{x}=\left(\frac{\cos\alpha}{1+\sin\alpha}+1\right)^{2}=\frac{2(1+\cos\alpha)}{1+\sin\alpha}.