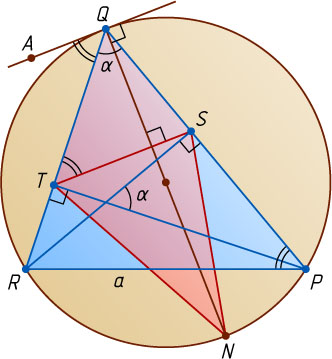
938. В остроугольном треугольнике PQR
(PQ\gt QR)
проведены высоты PT
и RS
; QN
— диаметр окружности, описанной около треугольника PQR
. Известно, что острый угол между высотами PT
и RS
равен \alpha
, PR=a
. Найдите площадь четырёхугольника NSQT
.
Ответ. \frac{1}{2}a^{2}\ctg\alpha
.
Указание. Диагонали четырёхугольника NSQT
перпендикулярны (см. задачу 480).
Решение. Треугольник PQR
— остроугольный, поэтому его угол при вершине Q
равен острому углу между высотами PT
и RS
, т. е. \alpha
.
Через вершину Q
проведём касательную к описанной окружности треугольника PQR
и отметим на ней точку A
, лежащую с точкой P
по разные стороны от прямой QR
. Из теоремы об угле между касательной и хордой следует, что \angle AQR=\angle RPQ=\angle QTS
, значит, ST\parallel AQ
, а так как QN\perp AQ
, то ST\perp QN
. Таким образом, диагонали четырёхугольника NSQT
перпендикулярны. Тогда, если S
— его площадь, то S=\frac{1}{2}ST\cdot QN
.
Треугольник TQS
подобен треугольнику PQR
, причём коэффициент подобия равен \frac{QT}{QP}=\cos\alpha
(см. задачу 19), значит, ST=PR\cos\alpha=a\cos\alpha
.
Пусть r
— радиус описанной окружности треугольника PQR
. Тогда r=\frac{PR}{2\sin\alpha}=\frac{a}{2\sin\alpha}
. Следовательно,
S=\frac{1}{2}ST\cdot QN=\frac{1}{2}a\cos\alpha\cdot2r=\frac{1}{2}a\cos\alpha\cdot\frac{a}{\sin\alpha}=\frac{1}{2}a^{2}\ctg\alpha.