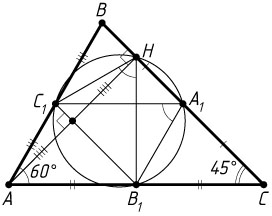
10203. В треугольнике ABC
точки A_{1}
, B_{1}
и C_{1}
— середины сторон BC
, AC
и AB
соответственно, AH
— высота, \angle BAC=60^{\circ}
, \angle BCA=45^{\circ}
.
а) Докажите, что точки A_{1}
, B_{1}
, C_{1}
и H
лежат на одной окружности.
б) Найдите A_{1}H
, если BC=2\sqrt{3}
.
Ответ. 1.
Решение. а) Отрезки A_{1}C_{1}
и A_{1}B_{1}
— средние линии треугольника ABC
, поэтому
A_{1}C_{1}\parallel AB_{1},~A_{1}B_{1}\parallel AC_{1}.
Значит, AB_{1}A_{1}C_{1}
— параллелограмм. Следовательно, \angle B_{1}A_{1}C_{1}=\angle B_{1}AC_{1}
.
Отрезок B_{1}C_{1}
— средняя линия треугольника ABC
, поэтому B_{1}C_{1}\parallel BC
и B_{1}C_{1}\perp AH
. По теореме Фалеса прямая B_{1}C_{1}
проходит через середину высоты AH
, значит, углы B_{1}HC_{1}
и B_{1}AC_{1}
симметричны относительно прямой B_{1}C_{1}
, а следовательно, они равны.
Таким образом, из точек A_{1}
и H
, лежащих по одну сторону от прямой B_{1}C_{1}
, отрезок B_{1}C_{1}
виден под одним и тем же углом. Следовательно, точки A_{1}
, B_{1}
, C_{1}
и H
лежат на одной окружности (см. задачу 12).
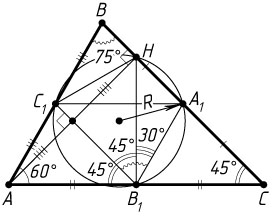
б) Пусть R
— радиус этой окружности. По теореме синусов (см. задачу 23)
R=\frac{B_{1}C_{1}}{2\sin\angle B_{1}A_{1}C_{1}}=\frac{\sqrt{3}}{2\sin60^{\circ}}=1.
Из симметрии
\angle HB_{1}C_{1}=\angle AB_{1}C_{1}=\angle ACB=45^{\circ}.
Тогда
\angle A_{1}B_{1}H=\angle A_{1}B_{1}C_{1}-\angle HB_{1}C_{1}=75^{\circ}-45^{\circ}=30^{\circ}.
Следовательно, по теореме синусов
A_{1}H=2R\sin\angle A_{1}B_{1}H=2R\sin30^{\circ}=2\cdot1\cdot\frac{1}{2}=1.