3380. В треугольнике ABC
проведены высоты BM
и CN
, O
— центр вписанной окружности. Известно, что BC=24
, MN=12
. Найдите радиус окружности, описанной около треугольника BOC
.
Ответ. 8\sqrt{3}
или 24.
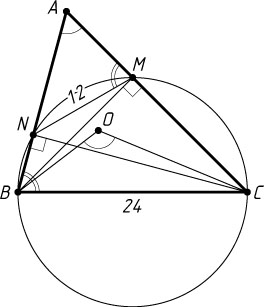
Решение. Из точек M
и N
сторона BC
видна под прямым углом, значит, эти точки лежат на окружности с диаметром BC
.
Пусть угол BAC
— острый (рис. 1). Четырёхугольник BNMC
— вписанный, поэтому
\angle NBC=180^{\circ}-\angle NMC=\angle AMN.
Треугольник AMN
подобен треугольнику ABC
по двум углам (угол A
— общий), причём коэффициент подобия равен \frac{AN}{AC}=\cos\angle BAC
(см. задачу 19). В то же время, коэффициент подобия равен \frac{MN}{BC}=\frac{12}{24}=\frac{1}{2}
, поэтому \cos\angle BAC=\frac{1}{2}
. Тогда \angle BAC=60^{\circ}
.
Центр O
окружности, вписанной в треугольник ABC
— точка пересечения биссектрис треугольника. Сумма углов при вершинах B
и C
треугольника ABC
равна 120^{\circ}
, а сумма их половин (т. е. сумма углов при вершинах B
и C
треугольника BOC
) равна 60^{\circ}
, значит, \angle BOC=180^{\circ}-60^{\circ}=120^{\circ}
.
Пусть R
— радиус окружности, описанной около треугольника BOC
. По теореме синусов
R=\frac{BC}{2\sin\angle BOC}=\frac{24}{2\sin120^{\circ}}=\frac{12}{\frac{\sqrt{3}}{2}}=\frac{24}{\sqrt{3}}=8\sqrt{3}.
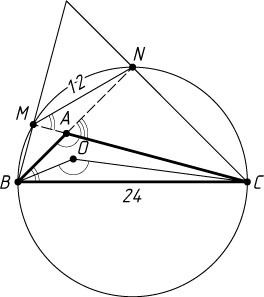
Пусть теперь угол BAC
— тупой (рис. 2). Тогда вписанные углы CMN
и CBN
опираются на одну и ту же дугу, поэтому \angle AMN=\angle CMN=\angle CBN=\angle ABC
, значит, треугольник AMN
подобен треугольнику ABC
, причём коэффициент подобия равен \frac{AN}{AC}=\cos\angle CAN
. В то же время, коэффициент подобия равен \frac{MN}{BC}=\frac{12}{24}=\frac{1}{2}
, поэтому \cos\angle CAN=\frac{1}{2}
. Значит, \angle CAN=60^{\circ}
. Следовательно,
\angle BAC=180^{\circ}-\angle CAN=120^{\circ},~\angle BOC=180^{\circ}-\frac{1}{2}(180^{\circ}-120^{\circ})=150^{\circ}.
Пусть R_{1}
— радиус окружности, описанной около треугольника BOC
. По теореме синусов
R=\frac{BC}{2\sin\angle BOC}=\frac{24}{2\sin150^{\circ}}=\frac{12}{\frac{1}{2}}=24.