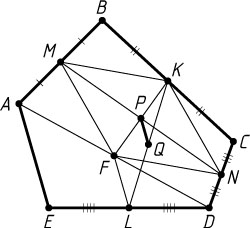
4517. Точки M
, K
, N
и L
— середины сторон соответственно AB
, BC
, CD
и DE
пятиугольника ABCDE
, P
и Q
— середины отрезков соответственно MN
и KL
. Докажите, что отрезок PQ
в четыре раза меньше стороны AE
и параллелен ей.
Указание. Воспользуйтесь векторным равенством
\overrightarrow{PQ}=\frac{1}{2}(\overrightarrow{MK}+\overrightarrow{NL})
или примените теорему о серединах сторон четырёхугольника (см. задачу 1204).
Решение. Первый способ. Из задачи 4504 следует, что
\overrightarrow{PQ}=\frac{1}{2}(\overrightarrow{MK}+\overrightarrow{NL})=\frac{1}{2}(\overrightarrow{MB}+\overrightarrow{BK}+\overrightarrow{ND}+\overrightarrow{DL})=
=\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{2}\overrightarrow{DE}\right)=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE})=\frac{1}{4}\overrightarrow{AE}.
Следовательно, PQ=\frac{1}{4}AE
и PQ\parallel AE
.
Второй способ. Пусть F
— середина AD
. Тогда четырёхугольник MKNF
— параллелограмм (см. задачу 1204). Его диагональ KF
проходит через середину P
его другой диагонали MN
. Отрезок PQ
— средняя линия треугольника KFL
, а отрезок FL
— средняя линия треугольника AED
. Следовательно,
PQ\parallel FL\parallel AE,~PQ=\frac{1}{2}FL=\frac{1}{2}\cdot\frac{1}{2}AE=\frac{1}{4}AE.
Примечание. Утверждение верно для любого пространственного пятиугольника.
