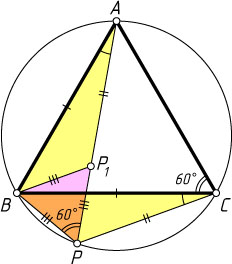
17. Теорема Помпею. На меньшей дуге BC
окружности, описанной около равностороннего треугольника ABC
, взята произвольная точка P
. Докажите, что AP=BP+CP
.
Указание. Отложите на луче AP
отрезок AP_{1}
, равный отрезку CP
, и докажите, что треугольник BPP_{1}
— равносторонний.
Решение. Первый способ. Отложим на луче AP
отрезок AP_{1}
, равный отрезку CP
. Тогда треугольники AP_{1}B
и CPB
равны по двум сторонам и углу между ними. В треугольнике BPP_{1}
BP_{1}=BP,~\angle BPP_{1}=\angle BPA=\angle BCA=60^{\circ}.
Поэтому PP_{1}=BP
. Следовательно,
AP=AP_{1}+P_{1}P=BP+CP.
Второй способ. Пусть P_{1}
— образ точки P
при повороте на 60^{\circ}
вокруг вершины B
, переводящем C
в A
. Тогда
\angle AP_{1}B+\angle BP_{1}P=\angle CPB+\angle BP_{1}P=120^{\circ}+60^{\circ}=180^{\circ}.
Поэтому точка P_{1}
лежит на отрезке AP
. Следовательно,
AP=AP_{1}+P_{1}P=BP+CP.
Третий способ. Обозначим AC=AB=BC=a
, CP=x
, BP=y
, AP=z
. Пусть x\ne y
. По теореме косинусов из треугольников ACP
и ABP
находим, что
a^{2}=x^{2}+z^{2}-xz,~a^{2}=y^{2}+z^{2}-yz.
Вычитая почленно эти уравнения, получим, что
(x-y)(x+y-z)=0.
Поскольку x\ne y
, то z=x+y
.
Если же x=y
, то угол CAP
прямоугольного треугольника ACP
равен 30^{\circ}
. Поэтому z=2x=x+y
.
Четвёртый способ. Поскольку четырёхугольник ABPC
— вписанный, то по теореме Птолемея (см. задачу 130)
BC\cdot AP=AC\cdot BP+AB\cdot CP,
а так как BC=AC=AB
, то AP=BP+CP
.
Пятый способ. Пусть угол между диагоналями четырёхугольника ABPC
равен \varphi
, а угловая величина меньшей дуги BP
равна \alpha
. Тогда
\varphi=\frac{1}{2}(120^{\circ}+\alpha)=\angle ACP.
Записав площадь четырёхугольника ABPC
двумя способами, получим равенство
\frac{1}{2}AP\cdot BC\sin\varphi=\frac{1}{2}AC\cdot CP\sin\angle ACP+\frac{1}{2}AB\cdot BP\sin(180^{\circ}-\angle ACP),
или
AP\cdot BC\sin\left(60^{\circ}+\frac{\alpha}{2}\right)=AC\cdot CP\sin\left(60^{\circ}+\frac{\alpha}{2}\right)+AB\cdot BP\sin\left(60^{\circ}+\frac{\alpha}{2}\right),
а так как AB=BC=AC
, то
AP=CP+BP.
Примечание. 1. Если точка P
не лежит на дуге BC
, то верно неравенство AP\lt BP+CP
.
2. См. статью М.Горелова «Теорема Птолемея и перекладывание треугольников», Квант, 2017, N1, с.33-35.
3. См. статью Е.Бакаева «Обобщение теоремы Помпею», Квант, 2017, N1, с.39-42.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 99, с. 104
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 66, с. 10
Источник: Московская математическая олимпиада. — 1940, VI, 2-й тур, 7-8 классы
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 5, с. 200
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — № 1, с. 56
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 11, с. 24
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 57, с. 11
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 57, с. 10
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 18.13, с. 70
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.14, с. 375
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 37, с. 8
Источник: Бабинская И. Л. Задачи математических олимпиад. — М.: Наука, 1975. — № 323, с. 36
Источник: Всесибирская физико-математическая олимпиада. — 2008-2009, первый этап, задача 5, 9 класс
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.96, с. 180; № 8.2, с. 65
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 521
