130. Теорема Птолемея. Докажите, что если четырёхугольник вписан в окружность, то сумма произведений длин двух пар его противоположных сторон равна произведению длин его диагоналей.
Указание. Основания перпендикуляров, опущенных из вершины D
четырёхугольника ABCD
на прямые AB
, BC
и AC
, лежат на одной прямой (прямая Симсона).
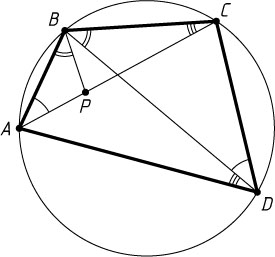
Решение. Первый способ. Пусть четырёхугольник ABCD
вписан в окружность (рис. 1). Отложим от луча BD
в полуплоскости, содержащей точку A
, луч BP
так, что \angle ABP=\angle CBD
(P
— на AC
).
Треугольники ABP
и DBC
подобны по двум углам. Поэтому
\frac{AB}{AP}=\frac{BD}{CD}~\Rightarrow~AB\cdot CD=AP\cdot BD.
Поскольку
\angle ABD=\angle ABP+\angle PBD=\angle CBD+\angle PBD=\angle PBC,~\angle BDA=\angle BCP,
треугольники PBC
и ABD
также подобны по двум углам. Поэтому
\frac{BC}{PC}=\frac{BD}{AD}~\Rightarrow~BC\cdot AD=PC\cdot BD.
Сложив почленно эти равенства, получим, что
AB\cdot CD+BC\cdot AD=AP\cdot BD+BD\cdot PC=BD\cdot(AP+PC)=BD\cdot AC.
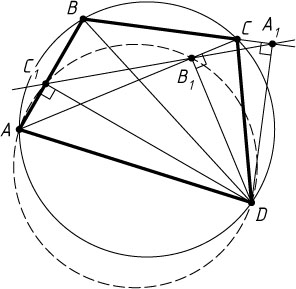
Второй способ. Пусть A_{1}
, B_{1}
и C_{1}
— основания перпендикуляров, опущенных из вершины D
вписанного четырёхугольника ABCD
на прямые BC
, AC
и AB
соответственно (рис. 2). Точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой — прямой Симсона треугольника ABC
(см. задачу 83).
Точки A
, B_{1}
, D
и C_{1}
лежат на окружности с диаметром AD
. Поэтому
B_{1}C_{1}=AD\sin\angle C_{1}AB_{1}=AD\sin\angle BAC=AD\cdot\frac{BC}{2R},
где R
— радиус окружности, описанной около данного четырёхугольника. Аналогично докажем, что
A_{1}B_{1}=CD\cdot\frac{AB}{2R},~A_{1}C_{1}=BD\cdot\frac{AC}{2R}.
Поскольку точка B_{1}
лежит между точками C_{1}
и A_{1}
, то
C_{1}B_{1}+B_{1}A_{1}=C_{1}A_{1}~\Rightarrow~AD\cdot\frac{BC}{2R}+CD\cdot\frac{AB}{2R}=BD\cdot\frac{AC}{2R}.
Следовательно,
AD\cdot BC+CD\cdot AB=BD\cdot AC.
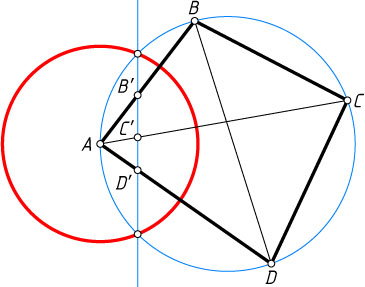
Третий способ. При инверсии относительно окружности произвольного радиуса R
с центром A
(рис. 3) описанная окружность четырёхугольника ABCD
, проходящая через центр инверсии, перейдёт в прямую, не проходящую через центр инверсии, а точки B
, C
и D
перейдут в точки B'
, C'
и D'
соответственно, лежащие на этой прямой, причём точка C'
лежит между B'
и D'
. Тогда B'D'=B'C'+C'D'
, а так как
B'D'=BD\cdot\frac{R^{2}}{AB\cdot AD},~B'C'=BC\cdot\frac{R^{2}}{AB\cdot AC},~C'D'=CD\cdot\frac{R^{2}}{AC\cdot AD},
то
BD\cdot\frac{R^{2}}{AB\cdot AD}=BC\cdot\frac{R^{2}}{AB\cdot AC}+CD\cdot\frac{R^{2}}{AC\cdot AD}.
Следовательно,
AC\cdot BD=AD\cdot BC+AB\cdot CD.
Что и требовалось доказать.
(Заметим, что если точки A
, B
, C
и D
не лежат на одной окружности, то точки B'
, C'
и D'
не лежат на одной прямой, поэтому B'D'\lt B'C'+C'D'
. Следовательно, AC\cdot BD\lt AD\cdot BC+AB\cdot CD
.)
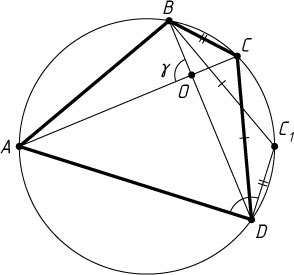
Четвёртый способ. Пусть четырёхугольник ABCD
вписан в окружность, а его диагонали AC
и BD
пересекаются в точке O
, причём \angle AOB=\gamma
(рис. 4). Тогда S_{ABCD}=\frac{1}{2}AC\cdot BD\sin\gamma
, причём угол \gamma
равен сумме половины дуги AB
, не содержащей точки C
, и половины дуги CD
, не содержащей точки A
.
Пусть C_{1}
— точка, симметричная вершине C
относительно серединного перпендикуляра к отрезку BD
. Тогда точка C_{1}
также лежит на окружности, четырёхугольники ABCD
и ABC_{1}D
равновелики, BC_{1}=DC
, DC_{1}=BC
, а угол ADC_{1}
равен сумме половины дуги AB
, не содержащей точки C_{1}
, и половины дуги BC_{1}
, не содержащей точки D
. Последняя дуга равна дуге CD
, не содержащей точки A
. Следовательно, \angle ADC_{1}=\gamma
, а \angle ABC_{1}=180^{\circ}-\gamma
.
Тогда
S_{ABCD}=S_{ABC_{1}D}=S_{\triangle ADC_{1}}+S_{\triangle ABC_{1}}=
=\frac{1}{2}AD\cdot DC_{1}\sin\gamma+\frac{1}{2}AB\cdot BC_{1}\sin(180^{\circ}-\gamma)=
=\frac{1}{2}AD\cdot BC\sin\gamma+\frac{1}{2}AB\cdot CD\sin\gamma=\frac{1}{2}(AD\cdot BC+AB\cdot CD)\sin\gamma.
Из равенства
\frac{1}{2}AC\cdot BD\sin\gamma=\frac{1}{2}(AD\cdot BC+AB\cdot CD)\sin\gamma
следует, что AC\cdot BD=AD\cdot BC+AB\cdot CD
. Что и требовалось доказать.
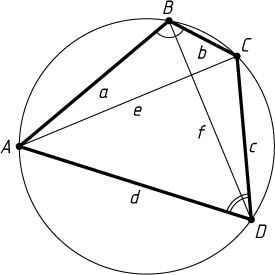
Пятый способ. Обозначим AB=a
, BC=b
, CD=c
, AD=d
, AC=e
, BD=f
(рис. 5). Из треугольников ABC
и ACD
по теореме косинусов находим, что
\cos\angle ABC=\frac{a^{2}+b^{2}-e^{2}}{2ab},~\cos\angle ADC=\frac{c^{2}+d^{2}-e^{2}}{2cd},
а так как \angle ABC+\angle ADC=180^{\circ}
, то \cos\angle ABC+\cos\angle ADC=0
, или
\frac{a^{2}+b^{2}-e^{2}}{2ab}+\frac{c^{2}+d^{2}-e^{2}}{2cd}=0.
Из этого равенства находим, что
e^{2}=\frac{cd(a^{2}+b^{2})+ab(c^{2}+d^{2})}{ab+cd}=\frac{(ac+bd)(ad+bc)}{ab+cd}.
Аналогично
f^{2}=\frac{(ab+cd)(ac+bd)}{ad+bc}.
Следовательно,
e^{2}f^{2}=(ac+bd)^{2},~ef=ac+bd.
Шестой способ. По теореме Бретшнейдера (см. задачу 5434)
(ef)^{2}=(ac)^{2}+(bd)^{2}-2abcd\cos(A+C).
Поскольку четырёхугольник вписанный, суммы его противоположных углов равны 180^{\circ}
, поэтому \cos(A+C)=\cos180^{\circ}=-1
. Значит,
(ef)^{2}=(ac)^{2}+(bd)^{2}+2abcd,~(ef)^{2}=(ac+bd)^{2}.
Следовательно, ef=ac+bd
.
Седьмой способ. Обозначим
AB=a,~BC=b,~CD=c,~AD=d,~AC=e,~BD=f,
\angle ADB=\angle ACB=\alpha,~\angle BDC=\angle BAC=\beta,
\angle CAD=\angle CBD=\gamma,~\angle ACD=\angle ABD=\delta
(рис. 6).
Рассмотрим треугольник A'B'C'
, подобный треугольнику ABC
с коэффициентом f
. Тогда
A'C'=ef,~A'B'=af,~B'C'=bf,~\angle B'A'C'=\beta,
\angle A'C'B'=\alpha,~\angle A'B'C'=\angle ABC=\gamma+\delta.
Вне треугольника A'B'C'
построим треугольник A'C''B'
, подобный треугольнику BCD
с коэффициентом a
. Тогда
A'B'=af,~A'C''=ab,~B'C''=ac,~\angle A'B'C''=\beta,
\angle B'A'C''=\gamma,~\angle A'C''B'=\angle BCD=\alpha+\delta.
Вне треугольника A'B'C'
построим треугольник B'A''C'
, подобный треугольнику DAB
с коэффициентом b
. Тогда
B'C'=bf,~A''B'=bd,~A''C'=ab,~\angle A''B'C'=\alpha,
\angle A''C'B'=\delta,~\angle B'A''C'=\angle DAB=\beta+\gamma.
Точка B'
лежит на отрезке A''B''
, так как
\angle A'B'C'+\angle A''B'C'+\angle C'B'A''=\beta+(\gamma+\delta)+\alpha=180^{\circ}
как половина суммы углов четырёхугольника ABCD
. Кроме того, A'C''=C'A''=ab
и A'C''\parallel C'A''
, поэтому A'C''A''C'
— параллелограмм. Следовательно,
ac+bd=B'C''+B'A''=A''C''=A'C'=ef.
Что и требовалось доказать.

Примечание. 1. Верно и обратное: если сумма произведений длин двух пар противоположных сторон четырёхугольника равна произведению длин его диагоналей, то около четырёхугольника можно описать окружность.
2. Для любого четырёхугольника ABCD
выполняется неравенство AC\cdot BD\leqslant AD\cdot BC+AB\cdot CD
, причём равенство достигается тогда и только тогда, когда четырёхугольник вписанный.
3. См. также статью В.Уроева «Инверсия», Квант, 1984, N5, с.26-32.
4. См. также статью М.Горелова «Теорема Птолемея и перекладывание треугольников», Квант, 2017, N1, с.33-35.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 215-216
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 56
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 258, с. 236
Источник: Тригг Ч. Задачи с изюминкой. — М.: Мир, 1975. — № 5, с. 14
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 328
Источник: Вступительный экзамен в МФТИ. — 1949, билет 20, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 49-20-5, с. 21
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 237, с. 65
Источник: Шень А. Х. Геометрия в задачах. — М.: МЦНМО, 2013. — № 778, с. 231
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 61, с. 263
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 242(б), с. 38
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.37, с. 155
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 595
Источник: Журнал «Квант». — 1984, № 5, с. 29, задача 2





