83. Докажите, что основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на одной прямой (прямая Симсона).
Решение. Первый способ. Пусть P
— точка описанной окружности треугольника ABC
, лежащая на дуге AC
, не содержащей точки B
(рис. 1); P_{1}
, P_{2}
, P_{3}
— основания перпендикуляров, опущенных из точки P
на прямые AB
, BC
, AC
соответственно.
Точки A
, P_{1}
, P
и P_{3}
лежат на окружности с диаметром AP
, поэтому
\angle P_{1}P_{3}A=\angle P_{1}PA.
Точки C
, P_{2}
, P_{3}
и P
лежат на окружности с диаметром PC
, поэтому
\angle P_{2}PC=\angle P_{2}P_{3}C.
Каждый из углов P_{1}PP_{2}
и APC
дополняет угол ABC
до 180^{\circ}
, поэтому
\angle P_{1}PP_{2}=\angle APC.
Тогда
\angle P_{1}PA=\angle P_{2}PC.
Значит,
\angle P_{1}P_{3}A=\angle P_{2}P_{3}C.
Следовательно, точки P_{1}
, P_{3}
и P_{2}
лежат на одной прямой.
Аналогично для любой другой точки P
, отличной от вершин треугольника ABC
.
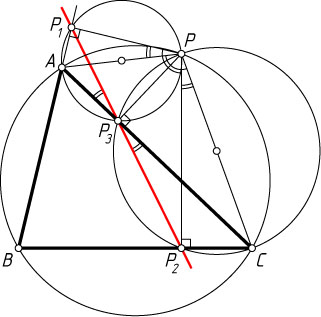
Второй способ. Пусть P
— точка описанной окружности треугольника ABC
, лежащая на дуге AC
, не содержащей точки B
(рис. 2); P_{1}
, P_{2}
, P_{3}
— основания перпендикуляров, опущенных из точки P
на прямые AB
, BC
, AC
соответственно.
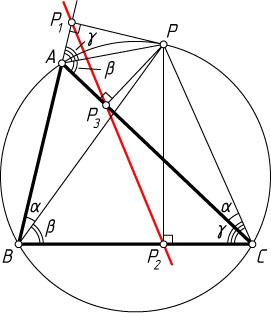
Обозначим \angle ABP=\alpha
, \angle CBP=\beta
, \angle BCP=\gamma
. Рассмотрим случай, когда все эти углы острые. Из прямоугольных треугольников CP_{2}P
и BP_{2}P
находим, что CP_{2}=PP_{2}\ctg\gamma
и P_{2}B=PP_{2}\ctg\beta
. Поэтому
\frac{CP_{2}}{P_{2}B}=\frac{PP_{2}\ctg\gamma}{PP_{2}\ctg\beta}=\frac{\ctg\gamma}{\ctg\beta}.
Учитывая, что
\angle PAP_{1}=180^{\circ}-\angle BAP=\angle BCP=\gamma,~\angle ACP=\angle ABP=\alpha,~\angle CAP=\angle CBP=\beta,
аналогично получим, что
\frac{BP_{1}}{P_{1}A}=\frac{PP_{1}\ctg\alpha}{PP_{1}\ctg\gamma}=\frac{\ctg\alpha}{\ctg\gamma},~\frac{AP_{3}}{P_{3}C}=\frac{PP_{3}\ctg\beta}{PP_{3}\ctg\alpha}=\frac{\ctg\beta}{\ctg\alpha}.
Поэтому
\frac{BP_{1}}{P_{1}A}\cdot\frac{AP_{2}}{P_{2}C}\cdot\frac{CP_{2}}{P_{2}B}=\frac{\ctg\alpha}{\ctg\gamma}\cdot\frac{\ctg\beta}{\ctg\alpha}\cdot\frac{\ctg\gamma}{\ctg\beta}=1.
Следовательно, по теореме Менелая (см. задачу 1622) точки P_{1}
, P_{2}
и P_{3}
лежат на одной прямой.
Аналогично для любой другой точки P
, отличной от вершин треугольника ABC
, и любых возможных \alpha
, \beta
, \gamma
.
Примечание. 1. Рассмотрения случаев можно избежать, рассматривая ориентированные углы (см. задачу 873).
2. Поскольку обратное утверждение также верно (см. задачу 6088), справедлива следующая теорема. Основания перпендикуляров, опущенных из некоторой точки на прямые, содержащие стороны треугольника, лежат на одной прямой тогда и только тогда, когда эта точка лежит на описанной окружности треугольника.
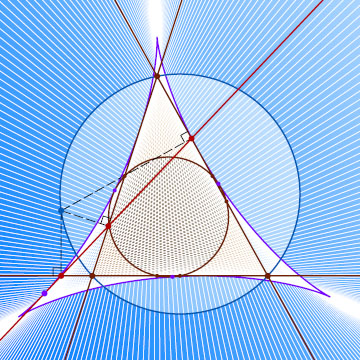
3. Все прямые Симсона треугольника ABC
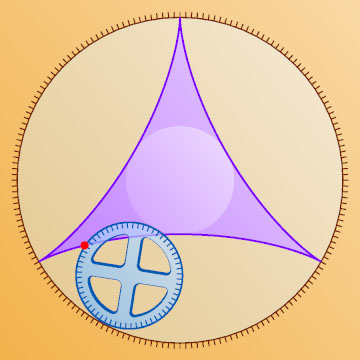
касаются одной кривой, называемой кривой Штейнера, или дельтоидой (рис. 3). Эта кривая представляет собой траекторию, по которой движется фиксированная точка окружности, в случае, когда эта окружность катится по окружности втрое большего радиуса, причём окружности касаются внутренним образом (рис. 4). Кривые такого типа называют гипоциклоидами. В нашем случае это кривая Штейнера, описанная около окружности девяти точек треугольника ABC
. (См. Васильев Н.Б., Гутенмахер В.Л. «Прямые и кривые», с.98, 106.)
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 72, с. 82
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 87, с. 11
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 159, с. 195
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 11, с. 33
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 124(а), с. 40
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.185(а), с. 116
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.105(а), с. 113
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 54
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 450, с. 54
Источник: Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М.: Наука, 1978. — № 7.23(а), с. 106
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 10.4, с. 79
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 39(а), с. 101
Источник: Всесибирская физико-математическая олимпиада. — 2008-2009, первый этап, задача 5, 11 класс




