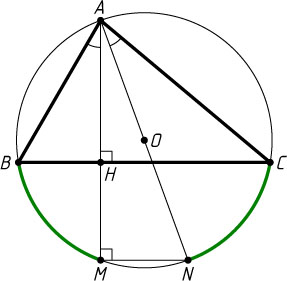
20. Вершина A
треугольника ABC
соединена отрезком с центром O
описанной окружности. Из вершины A
проведена высота AH
. Докажите, что \angle BAH=\angle OAC
.
Указание. Продолжите AH
и AO
до пересечения с окружностью.
Решение. Пусть A
— наибольший угол треугольника, AC\gt AB
, M
и N
— точки пересечения с окружностью лучей AH
и AO
. Тогда MN\parallel CB
. Поэтому \cup CN=\cup BM
. Следовательно,
\angle BAH=\angle BAM=\angle NAC=\angle OAC.
Аналогично для остальных случаев.
Примечание. Из этого утверждения следует, что точка пересечения высот треугольника и центр описанной окружности изогонально сопряжены относительно этого треугольника (см. замечание к задаче 4122).
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 70, с. 10
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 17, с. 184
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 111, с. 41
Источник: Дынкин Е. Б. и др. Математические задачи. — М.: Наука, 1966. — № 78, с. 17
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 25, с. 59; № 12, с. 97
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.1, с. 31
