4122. Три прямые, проходящие через вершины треугольника, пересекаются в одной точке. Докажите, что прямые, симметричные им относительно биссектрис соответствующих углов, также пересекаются в одной точке или параллельны.
Указание. См. задачи 4121 и 1621 (или 1900).
Решение. Первый способ. Пусть BC=a
, AC=b
и AB=c
— стороны треугольника ABC
; прямые, проходящие через вершины A
, B
и C
, пересекаются с прямыми соответственно BC
, AC
и AB
в точках A_{1}
, B_{1}
и C_{1}
, а симметричные им относительно биссектрис углов соответственно A
, B
и C
прямые пересекаются с прямыми BC
, AC
и AB
в точках A_{2}
, B_{2}
и C_{2}
соответственно. Тогда
\frac{BA_{1}\cdot BA_{2}}{CA_{1}\cdot CA_{2}}=\frac{c^{2}}{b^{2}},~\frac{CB_{1}\cdot CB_{2}}{AB_{1}\cdot AB_{2}}=\frac{a^{2}}{c^{2}},~\frac{AC_{1}\cdot AC_{2}}{BC_{1}\cdot BC_{2}}=\frac{b^{2}}{a^{2}}
(см. задачу 4121). Тогда
\left(\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}C}\right)\cdot\left(\frac{AC_{2}}{C_{2}B}\cdot\frac{BA_{2}}{A_{2}C}\cdot\frac{CB_{2}}{B_{2}C}\right)=
=\frac{BA_{1}\cdot BA_{2}}{CA_{1}\cdot CA_{2}}\cdot\frac{CB_{1}\cdot CB_{2}}{AB_{1}\cdot AB_{2}}\cdot\frac{AC_{1}\cdot AC_{2}}{BC_{1}\cdot BC_{2}}=
=\frac{c^{2}}{b^{2}}\cdot\frac{a^{2}}{c^{2}}\cdot\frac{b^{2}}{a^{2}}=1,
а так как прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке, то по теореме Чевы (см. задачу 1621)
\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}C}=1.
Значит,
\frac{AC_{2}}{C_{2}B}\cdot\frac{BA_{2}}{A_{2}C}\cdot\frac{CB_{2}}{B_{2}C}=1.
Следовательно, прямые AA_{2}
, BB_{2}
и CC_{2}
пересекаются в одной точке или параллельны (см. задачу 1621).
Второй способ. Пусть прямые, проходящие через вершины A
, B
и C
треугольника ABC
, пересекаются с прямыми соответственно BC
, AC
и AB
в точках A_{1}
, B_{1}
и C_{1}
, а симметричные им относительно биссектрис углов соответственно A
, B
и C
прямые пересекаются с прямыми BC
, AC
и AB
в точках A_{2}
, B_{2}
и C_{2}
соответственно.
Применив тригонометрическую форму теоремы Чевы для прямых AA_{1}
, BB_{1}
и CC_{1}
(см. задачу 1900), получим, что
\frac{\sin\angle BAA_{1}}{\sin\angle A_{1}AC}\cdot\frac{\sin\angle ACC_{1}}{\sin\angle C_{1}CB}\cdot\frac{\sin\angle CBB_{1}}{\sin\angle B_{1}BA}=1.
Заметим, что
\angle BAA_{2}=\angle A_{1}AC,~\angle A_{2}AC=\angle BAA_{1},
\angle ACC_{2}=\angle C_{1}CB,~\angle C_{2}CB=\angle ACC_{1},
\angle CBB_{2}=\angle B_{1}BA,~\angle B_{2}BA=\angle CBB_{1}.
Поэтому
\frac{\sin\angle BAA_{2}}{\sin\angle A_{2}AC}\cdot\frac{\sin\angle ACC_{2}}{\sin\angle C_{2}CB}\cdot\frac{\sin\angle CBB_{2}}{\sin\angle B_{2}BA}=\frac{\sin\angle A_{1}AC}{\sin\angle BAA_{1}}\cdot\frac{\sin\angle C_{1}CB}{\sin\angle ACC_{1}}\cdot\frac{\sin\angle B_{1}BA}{\sin\angle CBB_{1}}=
=\left(\frac{\sin\angle BAA_{1}}{\sin\angle A_{1}AC}\cdot\frac{\sin\angle ACC_{1}}{\sin\angle C_{1}CB}\cdot\frac{\sin\angle CBB_{1}}{\sin\angle B_{1}BA}\right)^{-1}=1.
Следовательно, прямые AA_{2}
, BB_{2}
и CC_{2}
пересекаются в одной точке или параллельны (см. задачу 1900).
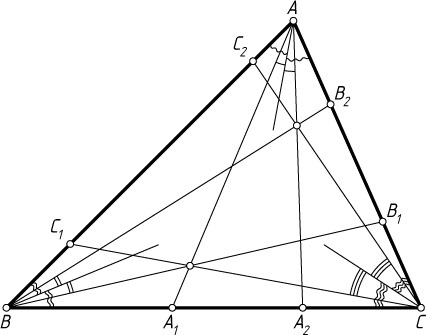
Примечание. Две прямые, проходящие через вершину угла и образующие равные углы с биссектрисой угла, называются изогональными прямыми относительно сторон этого угла.
Утверждение задачи можно сформулировать так. Если три прямые, проходящие через вершины треугольника, пересекаются в одной точке, то изогональные им относительно сторон соответствующих углов прямые также пересекаются в одной точке или параллельны.
Точка пересечения данных трёх прямых и точка пересечения изогональных прямых называются изогонально сопряжёнными относительно данного треугольника.
Например, симедианы треугольника, т. е. прямые, изогональные медианам треугольника (см. задачу 4121), пересекаются в одной точке — точке Лемуана. Точка пересечения медиан треугольника и точка Лемуана — изогонально сопряжённые точки.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 343, с. 41
