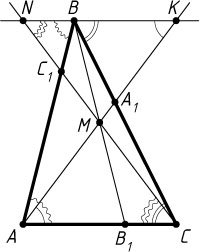
1621. Теорема Чевы. Пусть точки A_{1}
, B_{1}
и C_{1}
принадлежат сторонам (или их продолжениям) соответственно BC
, AC
и AB
треугольника ABC
. Докажите, что прямые AA_{1}
, BB_{1}
, CC_{1}
пересекаются в одной точке или параллельны тогда и только тогда, когда
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Указание. Проведите через вершину B
прямую, параллельную AC
, продолжите до пересечения с этой прямой отрезки AA_{1}
и CC_{1}
и рассмотрите образовавшиеся пары подобных треугольников.
Решение. Первый способ. Рассмотрим случай, когда точки A_{1}
, B_{1}
и C_{1}
лежат на сторонах треугольника, а не на их продолжениях. Пусть отрезки AA_{1}
, BB_{1}
и CC_{1}
пересекаются в точке M
. Проведём через вершину B
прямую, параллельную AC
, и продолжим отрезки AA_{1}
и CC_{1}
до пересечения с этой прямой в точках K
и N
соответственно.
Из подобия треугольников BA_{1}K
и CA_{1}A
следует, что
BK=AC\cdot\frac{BA_{1}}{A_{1}C}.
Аналогично
BN=AC\cdot\frac{BC_{1}}{C_{1}A}.
Тогда
\frac{AB_{1}}{BK}=\frac{B_{1}M}{MB}=\frac{CB_{1}}{BN}.
Следовательно,
\frac{AB_{1}}{B_{1}C}=\frac{BK}{BN}=\frac{\frac{BA_{1}}{A_{1}C}}{\frac{BC_{1}}{C_{1}A}}=\frac{BA_{1}}{A_{1}C}\cdot\frac{C_{1}A}{BC_{1}}.
Поэтому
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Пусть теперь
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Предположим, что прямая, проходящая через вершину B
и точку пересечения отрезков AA_{1}
и CC_{1}
, пересекает сторону AC
в точке P
. Тогда по доказанному
\frac{AP}{PC}=\frac{BA_{1}}{A_{1}C}\cdot\frac{AC_{1}}{C_{1}B},
а так как по условию
\frac{AB_{1}}{B_{1}C}=\frac{BA_{1}}{A_{1}C}\cdot\frac{AC_{1}}{C_{1}B},
то
\frac{AP}{PC}=\frac{AB_{1}}{B_{1}C}.
Следовательно, точки P
и B_{1}
совпадают.
Аналогично для любого другого расположения точек A_{1}
, B_{1}
и C_{1}
на прямых BC
, AC
и AB
соответственно.
Второй способ. Пусть отрезки AA_{1}
, BB_{1}
и CC_{1}
пересекаются в точке M
. Применив теорему Менелая к треугольнику ACA_{1}
и прямой BB_{1}
, а также к треугольнику ABA_{1}
и прямой CC_{1}
, получим, что
\frac{AB_{1}}{B_{1}C}\cdot\frac{CB}{BA_{1}}\cdot\frac{A_{1}M}{MA}=1,
\frac{AC_{1}}{C_{1}B}\cdot\frac{BC}{CA_{1}}\cdot\frac{A_{1}M}{MA}=1.
Разделим почленно первое из этих равенств на второе. Получим:
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Обратно: пусть
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Предположим, что прямая, проходящая через вершину B
и точку пересечения отрезков AA_{1}
и CC_{1}
, пересекает сторону AC
в точке P
. Тогда по доказанному
\frac{AP}{PC}=\frac{BA_{1}}{A_{1}C}\cdot\frac{C_{1}A}{BC_{1}},
а так как по условию
\frac{AB_{1}}{B_{1}C}=\frac{BA_{1}}{A_{1}C}\cdot\frac{AC_{1}}{C_{1}B},
то
\frac{AP}{PC}=\frac{AB_{1}}{B_{1}C}.
Следовательно, точки P
и B_{1}
совпадают.
Третий способ. Пусть прямые AA_{1}
и CC_{1}
пересекаются в точке M
. Обозначим \frac{AC_{1}}{C_{1}B}=p
, \frac{BA_{1}}{A_{1}C}=q
. Нужно доказать, что прямая BB_{1}
проходит через точку M
тогда и только тогда, когда \frac{CB_{1}}{B_{1}C}=\frac{1}{pq}
.
Поместим в точки A
, B
и C
массы 1, p
и q
соответственно. Тогда C_{1}
— центр масс точек A
и B
, а A_{1}
— центр масс точек B
и C
(см. задачу 6798). Центр масс точек A
, B
и C
с данными массами лежит и на отрезке AA_{1}
и и на отрезке CC_{1}
, т. е. совпадает с M
.
С другой стороны, точка M
лежит на отрезке, соединяющем точку B
с центром масс точек A
и C
, т. е. с точкой, лежащей на стороне AC
и делящей её в отношении \frac{CB_{1}}{B_{1}A}=\frac{1}{pq}
.
Остаётся заметить, что на отрезке AC
существует единственная точка, делящая его в данном отношении \frac{CB_{1}}{B_{1}A}
.
Примечание. 1. См. также статью Б.Эрдниева и Н.Манцаева: «Теоремы Чевы и Менелая», Квант, 1990, N3, с.56-59.
2. Тригонометрическая форма теоремы Чевы. Пусть точки A_{1}
, B_{1}
и C_{1}
принадлежат сторонам (или их продолжениям) соответственно BC
, AC
и AB
треугольника ABC
. Обозначим \angle BAA_{1}=\alpha_{1}
, \angle A_{1}AC=\alpha_{2}
, \angle CBB_{1}=\beta_{1}
, \angle B_{1}BA=\beta_{2}
, \angle ACC_{1}=\gamma_{1}
, \angle C_{1}CB=\gamma_{2}
(имеются в виду ориентированные углы). Прямые AA_{1}
, BB_{1}
, CC_{1}
пересекаются в одной точке или параллельны тогда и только тогда, когда
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=1.
3. См. также статью А.Егорова «Теоремы Чевы и Менелая», Квант, 2004, N3, с.35-38.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 187-188
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 50(б), с. 96
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 133, с. 48
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 9-11
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 66
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 59, с. 104
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 607
Источник: Журнал «Crux Mathematicorum». — 1977, № 1, с. 2
