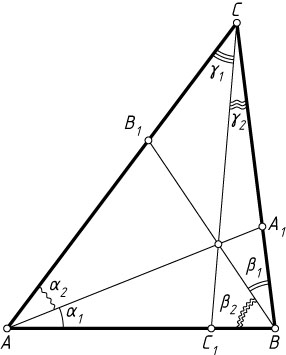
1900. Тригонометрическая форма теоремы Чевы. Пусть точки A_{1}
, B_{1}
и C_{1}
принадлежат сторонам (или их продолжениям) соответственно BC
, AC
и AB
треугольника ABC
. Обозначим \angle BAA_{1}=\alpha_{1}
, \angle A_{1}AC=\alpha_{2}
, \angle CBB_{1}=\beta_{1}
, \angle B_{1}BA=\beta_{2}
, \angle ACC_{1}=\gamma_{1}
, \angle C_{1}CB=\gamma_{2}
(имеются в виду ориентированные углы). Докажите, что прямые AA_{1}
, BB_{1}
, CC_{1}
пересекаются в одной точке или параллельны тогда и только тогда, когда
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=1.
Указание. Примените теорему синусов и теорему Чевы.
Решение. Предположим, что прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке. Докажем, что
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=1.
Действительно, по теореме Чевы (см. задачу 1621)
\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}=1.
Применяя теорему синусов к треугольникам ACC_{1}
и BCC_{1}
, получим, что
\frac{\sin\gamma_{1}}{AC_{1}}=\frac{\sin\angle AC_{1}C}{AC},~\frac{\sin\gamma_{2}}{C_{1}B}=\frac{\sin\angle BC_{1}C}{BC}=\frac{\sin\angle AC_{1}C}{BC},
откуда \frac{AC_{1}}{C_{1}B}=\frac{AC}{BC}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}
.
Аналогично
\frac{BA_{1}}{A_{1}C}=\frac{AB}{AC}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}},~~\frac{CB_{1}}{B_{1}A}=\frac{BC}{AB}\cdot\frac{\sin\alpha_{1}}{\sin\alpha_{2}}.
Следовательно,
1=\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}=\frac{AC}{BC}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}\cdot\frac{AB}{AC}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{BC}{AB}\cdot\frac{\sin\alpha_{1}}{\sin\alpha_{2}}=\frac{\sin\gamma_{1}}{\sin\gamma_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\alpha_{1}}{\sin\alpha_{2}}.
Что и требовалось доказать.
Обратно, пусть
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=1.
Докажем, что если при этом прямые AA_{1}
, BB_{1}
и CC_{1}
не параллельны, то они пересекаются в одной точке. Рассуждая аналогично предыдущему, получим, что
\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}=1.
Следовательно, прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке. Что и требовалось доказать.
Аналогично для любого другого расположения точек A_{1}
, B_{1}
и C_{1}
на прямых BC
, AC
и AB
соответственно.
Примечание. См. также статью А.Егорова «Теоремы Чевы и Менелая», Квант, 2004, N3, с.35-38.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 67
