22. С помощью одной линейки опустите перпендикуляр из данной точки на прямую, содержащую данный диаметр данной окружности, если:
а) точка не лежит ни на окружности, ни на данной прямой;
б) точка лежит на окружности или на данной прямой.
Указание. а) Соедините данную точку с концами данного диаметра и воспользуйтесь теоремой о высотах треугольника.
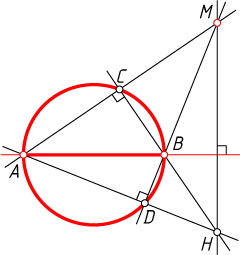
Решение. а) Соединим данную точку M
с концами данного диаметра AB
. Если прямая AM
вторично пересекает окружность в точке C
, а прямая BM
— в точке D
, то высоты треугольника AMB
лежат на прямых AD
и BC
. Пусть эти прямые пересекаются в точке H
. Тогда третья высота треугольника AMB
также проходит через точку H
, так как прямые, содержащие высоты треугольника, пересекаются в одной точке. Следовательно, прямая MH
перпендикулярна прямой AB
.
б) Через две точки, не лежащие ни на окружности, ни на прямой, проведём прямые l_{1}
и l_{2}
, перпендикулярные данной прямой (см. пункт (а)). Затем через данную точку проведём прямую, параллельную l_{1}
и l_{2}
(см. задачу 1540).
Источник: Колмогоров А. Н. и др. Геометрия: Учебное пособие для 8 кл. средней школы. — 3-е изд. — М.: Просвещение, 1975. — № 9, с. 41
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 58 (фрагмент), с. 23
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 13
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.36, с. 63
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.37, с. 60
Источник: Бабинская И. Л. Задачи математических олимпиад. — М.: Наука, 1975. — № 294, с. 34
