1540. Даны две параллельные прямые l
и l_{1}
. С помощью одной линейки проведите через данную точку M
прямую, параллельную прямым l
и l_{1}
.
Указание. Примените замечательное свойство трапеции.
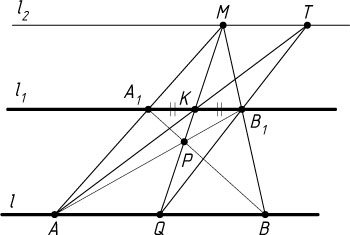
Решение. Пусть сначала точка M
и прямая l
лежат по разные стороны от прямой l_{1}
. Возьмём на на прямой l
две точки A
и B
. Пусть A_{1}
и B_{1}
— точки пересечения MA
и MB
с прямой l_{1}
, P
— точка пересечения диагоналей AB_{1}
и BA_{1}
трапеции AA_{1}B_{1}B
, K
и Q
— точки пересечения прямой MP
с A_{1}B_{1}
и AB
соответственно. Тогда Q
и K
— середины AB
и A_{1}B_{1}
(см. задачу 1513). Если T
— точка пересечения прямых AK
и QB_{1}
, то прямая TM
— искомая.
Действительно, треугольник KTB_{1}
подобен треугольнику ATQ
, а треугольник A_{1}MK
— треугольнику AMQ
, причём коэффициент подобия один и тот же, так как A_{1}K=KB_{1}
. Следовательно,
\frac{TB_{1}}{TQ}=\frac{KB_{1}}{AQ}=\frac{KA_{1}}{AQ}=\frac{MK}{MQ}.
Поэтому MT\parallel KB_{1}\parallel l
.
Если точка M
лежит внутри полосы между прямыми l
и l_{1}
, то через произвольную точку M_{1}
, лежащую вне этой полосы, проведём прямую l_{2}
, параллельную прямым l_{1}
и l
(указанным выше способом), а затем через точку M
проведём прямую, параллельную прямым l_{1}
и l_{2}
.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 57, с. 23
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 8.77, с. 206
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.81, с. 203
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 10.14, с. 80
