1513. Замечательное свойство трапеции. Докажите, что точка пересечения продолжений боковых сторон трапеции, середины оснований и точка пересечения диагоналей лежат на одной прямой.
Указание. Докажите, что прямая, проходящая через точку пересечения продолжений боковых сторон (или точку пересечения диагоналей) и середину одного из оснований, проходит через середину другого основания.
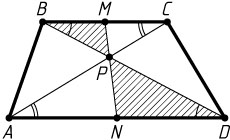
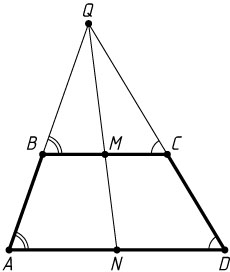
Решение. Первый способ. Пусть Q
— точка пересечения продолжений боковых сторон AB
и CD
трапеции ABCD
, M
— середина меньшего основания BC
, P
— точка пересечения диагоналей AC
и BD
, N
— точка пересечения прямой QM
с большим основанием AD
.
Из подобия треугольников QBM
и QAN
следует, что \frac{QM}{QN}=\frac{BM}{AN}
, а из подобия треугольников QCM
и QDN
— \frac{QM}{QN}=\frac{CM}{DN}
. Поэтому \frac{BM}{AN}=\frac{CM}{DN}
, а так как BM=CM
, то AN=DN
, т. е. N
— середина AD
.
Аналогично докажем, что прямая, проходящая через точку P
пересечения диагоналей и середину одного из оснований, проходит через середину другого основания.
Второй способ. При гомотетии с центром в точке P
пересечения диагоналей AC
и BD
, переводящей вершину B
трапеции ABCD
в вершину D
, точка C
переходит в точку A
, основание BC
— в основание DA
, середина M
основания BC
— в середину N
основания DA
. Следовательно, прямая MN
проходит через центр гомотетии, т. е. через точку P
.
Аналогично докажем, что прямая MN
проходит через точку пересечения прямых AB
и DC
.
Примечание. Это утверждение — частный случай теоремы о пропорциональных отрезках на параллельных прямых (см. задачу 1597).
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 10, с. 196
Источник: Вступительный экзамен в МФТИ. — 1951, билет 15, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 51-15-1, с. 33
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 28
Источник: Болтянский В. Г., Яглом И. М. Преобразования. Векторы. — М.: Просвещение, 1964. — № 348, с. 149
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 397, с. 60
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 19.2, с. 389

