28. Точки A
, B
, C
и D
лежат на окружности. Точки M
, N
, K
и L
— середины дуг AB
, BC
, CD
и DA
, последовательно расположенных на окружности. Докажите, что хорды MK
и NL
перпендикулярны.
Указание. Равные смежные углы — прямые.
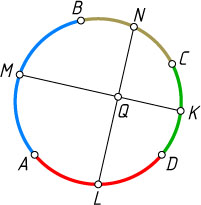
Решение. Пусть хорды MK
и NL
пересекаются в точке Q
. Каждый из двух смежных углов MQN
и MQL
равен полусумме противоположных дуг, высекаемых на окружности данными хордами (см. задачу 26). Эти полусуммы равны, так как состоят из соответственно равных слагаемых, а равные смежные углы — прямые.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 343, с. 292
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.18, с. 33
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.5, с. 16; № 66, c144
