29. По стороне правильного треугольника катится окружность радиуса, равного высоте треугольника. Докажите, что угловая величина дуги, высекаемой на окружности сторонами треугольника, всегда равна 60^{\circ}
.
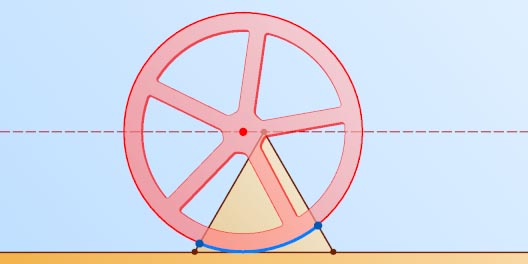
Указание. Рассмотрите угол между пересекающимися хордами, лежащими на прямых AB
и AC
.
Решение. Пусть окружность катится по стороне BC
треугольника ABC
. Тогда угол BAC
равен полусумме двух равных дуг (см. задачу 26).
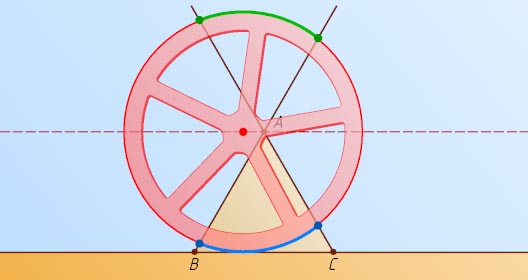
Примечание. Верно более общее утверждение. Пусть ABC
— равнобедренный треугольник (AB=AC
), AD
— его высота. Окружность радиуса AD
катится по прямой BC
. Тогда, пока вершина A
находится внутри окружности, дуга окружности, расположенная внутри треугольника, имеет постоянную длину.
Действительно, пусть KL
— дуга окружности, расположенная внутри треугольника ABC
. Продолжив стороны AC
и AB
за точку A
, получим дугу MN
, симметричную дуге KL
относительно диаметра, параллельного BC
. Поскольку угол A
измеряется дугой, равной \frac{1}{2}(\smile KL+\smile MN)=\smile KL
(см. задачу 26), то дуга KL
имеет постоянную угловую величину, и ей соответствует центральный угол, равный углу A
.
Источник: Московская математическая олимпиада. — 1945, VIII, 2-й тур, 9-10 классы
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 16, с. 28
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.16, с. 33
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 593, с. 74

