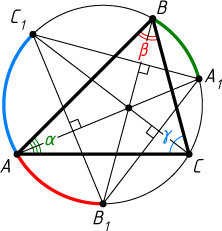
33. Продолжения биссектрис треугольника ABC
пересекают описанную окружность в точках A_{1}
, B_{1}
и C_{1}
соответственно. Докажите, что высоты треугольника A_{1}B_{1}C_{1}
лежат на прямых AA_{1}
, BB_{1}
и CC_{1}
.
Указание. Угол между хордами BB_{1}
и C_{1}A_{1}
равен полусумме дуг BA_{1}
и C_{1}AB_{1}
.
Решение. Обозначим
\angle BAC=\alpha,~\angle ABC=\beta,~\angle ACB=\gamma.
Угол между хордами BB_{1}
и C_{1}A_{1}
равен полусумме дуг BA_{1}
и C_{1}AB_{1}
(см. задачу 26). Поскольку
\smile BA_{1}=2\angle BAA_{1}=\alpha,
\smile C_{1}AB_{1}=\smile C_{1}A+\smile AB_{1}=2\angle ACC_{1}+2\angle ABB_{1}=\gamma+\beta,
то
\frac{1}{2}(\smile BA_{1}+\smile C_{1}AB_{1})=\frac{1}{2}(\alpha+\beta+\gamma)=\frac{1}{2}\cdot180^{\circ}=90^{\circ}.
Следовательно, BB_{1}\perp C_{1}A_{1}
.
Остальное аналогично.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.6, с. 16
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.20(а), с. 33
