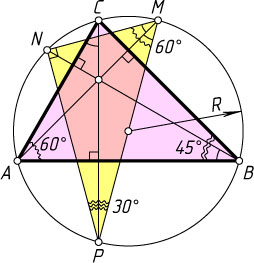
35. В треугольнике ABC
известно, что \angle A=60^{\circ}
, \angle B=45^{\circ}
. Продолжения высот треугольника ABC
пересекают описанную около него окружность в точках M
, N
, P
. Найдите отношение площадей треугольников ABC
и MNP
.
Ответ. \sqrt{2}\sin75^{\circ}=\frac{\sqrt{3}+1}{2}
.
Указание. Углы треугольника MNP
равны 60^{\circ}
, 90^{\circ}
, 30^{\circ}
.
Решение. Пусть продолжения высот треугольника ABC
, проведённых из вершин A
, B
и C
, пересекают описанную около него окружность в точках M
, N
и P
соответственно. В треугольнике MNP
\angle M=\angle NMP=\angle NMA+\angle PMA=\angle NBA+\angle ACP=
=(90^{\circ}-\angle A)+(90^{\circ}-\angle A)=30^{\circ}+30^{\circ}=60^{\circ}.
Аналогично \angle P=30^{\circ}
и \angle N=90^{\circ}
.
Пусть R
— радиус описанной окружности треугольника ABC
. Тогда
MN=2R\sin\angle P=2R\sin30^{\circ}=R,
NP=2R\sin\angle M=2R\sin60^{\circ}=R\sqrt{3},
S_{\triangle MNP}=\frac{1}{2}MN\cdot NP=\frac{R^{2}\sqrt{3}}{2};
AC=2R\sin\angle B=2R\sin45^{\circ}=R\sqrt{2},
BC=2R\sin\angle A=2R\sin60^{\circ}=R\sqrt{3},
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC\sin\angle C=R^{2}\cdot\frac{\sqrt{6}}{2}\cdot\sin75^{\circ}.
Следовательно,
\frac{S_{\triangle ABC}}{S_{\triangle MNP}}=\sqrt{2}\sin75^{\circ}.
Примечание. Если найдены углы M
, N
и P
, то можно воспользоваться формулами
S_{\triangle MNP}=2R^{2}\sin\angle M\sin\angle N\sin\angle P,
S_{\triangle ABC}=2R^{2}\sin\angle A\sin\angle B\sin\angle C
(см. задачу 4258).
Источник: Вступительный экзамен в МФТИ. — 1979, билет 2, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 79-2-4, с. 212
