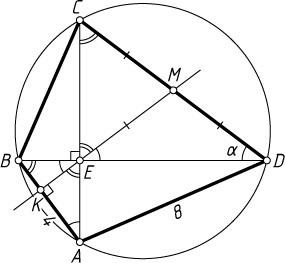
37. В окружность вписан четырёхугольник ABCD
, диагонали которого взаимно перпендикулярны и пересекаются в точке E
. Прямая, проходящая через точку E
и перпендикулярная к AB
, пересекает сторону CD
в точке M
. Докажите, что EM
— медиана треугольника CED
и найдите её длину, если AD=8
, AB=4
и \angle CDB=\alpha
.
Ответ. \frac{2\sqrt{4-\cos^{2}\alpha}}{\cos\alpha}
.
Указание. Докажите, что треугольник EMD
— равнобедренный.
Решение. Пусть K
— точка пересечения прямой EM
с отрезком AB
. Поскольку \angle BAC=\angle BDC
, то
\angle DEM=\angle BEK=\angle BAC=\angle CDE,
а так как
\angle ACD=\angle ABD=\angle ABE=\angle AEK=\angle MEC,
то DM=ME=MC
. Следовательно, EM
— медиана треугольника CED
(см. задачу 369).
По теореме Пифагора из треугольника AED
находим, что
DE^{2}=AD^{2}-AE^{2}=AD^{2}-AB^{2}\cdot\cos^{2}\angle BAC=64-16\cos^{2}\alpha.
Следовательно,
EM=\frac{1}{2}DC=\frac{DE}{2\cos\angle CDE}=\frac{4\sqrt{4-\cos^{2}\alpha}}{2\cos\alpha}=
=\frac{2\sqrt{4-\cos^{2}\alpha}}{\cos\alpha}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1979, № 3, вариант 1
