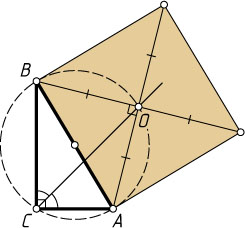
52. На гипотенузе AB
прямоугольного треугольника ABC
во внешнюю сторону построен квадрат с центром в точке O
. Докажите, что CO
— биссектриса прямого угла.
Указание. Точки A
, B
, C
и O
лежат на одной окружности.
Решение. Отрезок AB
виден из точек C
и O
под прямым углом. Поэтому точки A
, B
, C
и O
лежат на окружности с диаметром AB
. Углы ACO
и BCO
опираются на равные дуги этой окружности (см. задачу 805). Следовательно, CO
— биссектриса угла ACB
.
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 14, с. 31
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.93, с. 180
