53. На окружности даны точки A
, B
, C
, D
в указанном порядке; M
— середина дуги AB
. Обозначим точки пересечения хорд MC
и MD
с хордой AB
через E
и K
. Докажите, что KECD
— вписанный четырёхугольник.
Указание. \angle AEC=\frac{1}{2}(\smile MB+\smile ADC)
.
Решение. Заметим, что
\angle BEC=\frac{\smile AM+\smile BC}{2}
(см. задачу 26). Тогда, так как \smile MB=\smile AB
, то
\angle KDC=\angle MDC=\frac{\smile MBC}{2}=\frac{\smile MB+\smile BC}{2}=\frac{\smile AM+\smile BC}{2}=\angle BEC.
Значит,
\angle KEC+\angle KDC=(180^{\circ}-\angle BEC)+\angle BEC=180^{\circ}.
Следовательно, около четырёхугольника KECD
можно описать окружность.
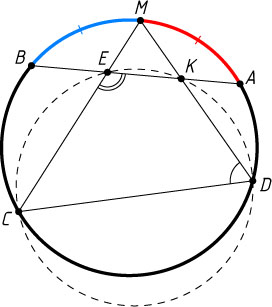
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 67, с. 81
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.14, с. 32
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.15, с. 32
