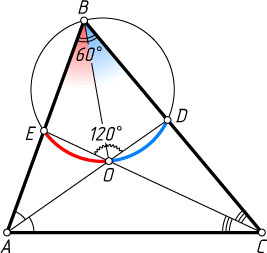
55. В треугольнике ABC
угол B
равен 60^{\circ}
, биссектрисы AD
и CE
пересекаются в точке O
. Докажите, что OD=OE
.
Указание. Найдите угол EOD
.
Решение. Поскольку
\angle EOD=\angle AOC=180^{\circ}-\frac{1}{2}(\angle BAC+\angle BCA)=
=180^{\circ}-\frac{1}{2}\cdot120^{\circ}=120^{\circ},
то точки B
, E
, O
и D
лежат на одной окружности. Биссектрисы треугольника пересекаются в одной точке, поэтому BO
— биссектриса угла DBE
. Значит, точка O
— середина дуги DOE
. Следовательно, OD=OE
(см. задачу 805).
Примечание. Верно также следующее утверждение. Если биссектрисы AD
и CE
треугольника ABC
пересекаются в точке O
, а OD=OE
, то либо \angle A=\angle C
, либо \angle B=60^{\circ}
(см. задачу 11242).
Источник: Всероссийская олимпиада школьников. — 1978-79, V, IV этап, 9 класс
Источник: Журнал «Квант». — 1979, № 10, с. 26, М586
Источник: Задачник «Кванта». — М586
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.33, с. 34
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.34, с. 34