57. Теорема Мансиона. Докажите, что отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.
Указание. Пусть вневписанная окружность касается стороны AB
треугольника ABC
. Точки A
, B
и центры O_{1}
и O_{2}
вписанной и вневписанной окружностей лежат на окружности с центром в середине отрезка O_{1}O_{2}
.
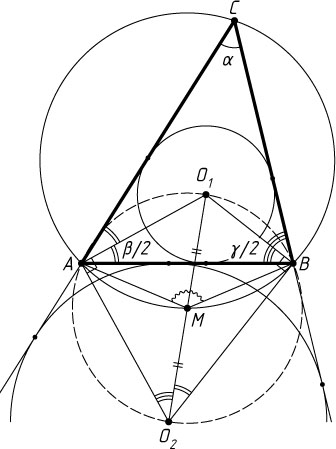
Решение. Первый способ. Пусть вневписанная окружность касается стороны AB
треугольника ABC
;
\angle C=\alpha,~\angle CAB=\beta,~\angle CBA=\gamma;
O_{1}
, O_{2}
— центры вписанной и вневписанной окружностей соответственно, M
— середина O_{1}O_{2}
.
Поскольку отрезок O_{1}O_{2}
виден из точек A
и B
под прямым углом, то M
— центр окружности, описанной около четырёхугольника AO_{1}BO_{2}
. Тогда
\angle AO_{2}B=\angle AO_{2}O_{1}+\angle BO_{2}O_{1}=\angle O_{1}BA+\angle O_{1}AB=\frac{\gamma}{2}+\frac{\beta}{2}=90^{\circ}-\frac{\alpha}{2},
\angle AMB=2\angle AO_{2}B=180^{\circ}-\alpha.
Следовательно, точки A
, C
, B
и M
лежат на одной окружности, т. е. на окружности, описанной около треугольника ABC
.
Второй способ. Пусть вневписанная окружность касается стороны AB
треугольника ABC
, O_{1}
и O_{2}
— центры вписанной и вневписанной окружностей соответственно.
Поскольку AO_{1}
и AO_{2}
— биссектрисы смежных углов, треугольник O_{1}AO_{2}
прямоугольный с гипотенузой O_{1}O_{2}
.
Пусть M
— точка пересечения описанной окружности треугольника ABC
с отрезком O_{1}O_{2}
. Тогда треугольник AO_{1}M
— равнобедренный, MO_{1}=MA
(см. задачу 788), а так как \angle MAO_{1}=\angle MO_{1}A
, то AM
— медиана треугольника O_{1}AO_{2}
(см. задачу 1483). Следовательно, M
— середина O_{1}O_{2}
.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — № 5, с. 23
Источник: Московская математическая олимпиада. — 1949, XII, 1-й тур, 7-8 классы
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 34, с. 185
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 5.2, с. 47
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 1, с. 34
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.132(б), с. 117
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.109(б), с. 119
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 4, с. 55
