58. Вписанная окружность касается сторон AB
и AC
треугольника ABC
в точках M
и N
. Пусть P
— точка пересечения прямой MN
и биссектрисы угла B
. Докажите, что \angle BPC=90^{\circ}
.
Указание. Точки N
, P
, C
и центр O
вписанной окружности лежат на окружности с диаметром OC
.
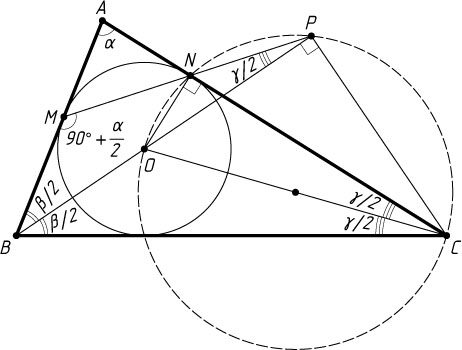
Решение. Пусть O
— центр вписанной окружности; \alpha
, \beta
, \gamma
— углы треугольника при вершинах A
, B
, C
соответственно. Тогда в треугольнике MPB
известно, что
\angle PBM=\frac{\beta}{2},~\angle BMP=90^{\circ}+\frac{\alpha}{2}.
Поэтому
\angle MPB=180^{\circ}-\frac{\beta}{2}-\left(90^{\circ}+\frac{\alpha}{2}\right)=90^{\circ}-\frac{\beta}{2}-\frac{\alpha}{2}=\frac{\gamma}{2}.
Следовательно, отрезок ON
виден из точек P
и C
под одним углом. Значит, точки O
, N
, P
и C
лежат на одной окружности, а так как ON\perp AC
, то OC
— диаметр этой окружности. Следовательно, \angle BPC=\angle OPC=90^{\circ}
.
Примечание. 1. Верно и обратное утверждение (см. задачу 6699).
2. Аналогичное утверждение верно для вневписанной окружности. Если вневписанная окружность треугольника ABC
касается стороны AB
в точке M
, продолжения стороны AC
— в точке N
, а P
— точка пересечения прямой MN
и биссектрисы внешнего угла треугольника ABC
при вершине B
, что \angle BPC=90^{\circ}
.
Доказательство. Пусть D
— центр указанной вневписанной окружности; \alpha
, \beta
, \gamma
— углы треугольника при вершинах A
, B
, C
соответственно. Тогда
\angle BMP=\angle AMN=\angle ANM=\frac{\alpha}{2},~\angle DPN=\angle BPM=180^{\circ}-\angle PBM-\angle BMP=
=180^{\circ}-\left(\beta+\frac{180^{\circ}-\beta}{2}\right)-\frac{\alpha}{2}=90^{\circ}-\frac{\beta}{2}-\frac{\alpha}{2}=\frac{\gamma}{2}=\angle DCN.
Следовательно, отрезок DN
виден из точек P
и C
под одним углом. Значит, точки D
, N
, P
и C
лежат на одной окружности, а так как DN\perp CN
, то DC
— диаметр этой окружности. Следовательно, \angle BPC=90^{\circ}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.41(a), с. 35
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.44(а), с. 35
Источник: Польские математические олимпиады. — 1994, второй тур, задача 5
Источник: Всесибирская физико-математическая олимпиада. — 2014-2015, первый этап, задача 4, 10 класс
