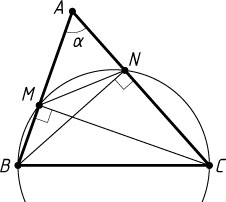
59. На стороне BC
треугольника ABC
как на диаметре построена окружность, пересекающая стороны AB
и AC
в точках M
и N
. Найдите площадь треугольника AMN
, если площадь треугольника ABC
равна S
, а угол BAC
равен \alpha
.
Ответ. S\cos^{2}\alpha
.
Указание. Треугольник MAN
подобен треугольнику CAB
(см. задачу 19).
Решение. CM
и BN
— высоты треугольника ABC
. Треугольник MAN
подобен треугольнику CAB
с коэффициентом подобия \frac{AN}{AB}=\cos\alpha
(см. задачу 19), поэтому
S_{\triangle AMN}=\left(\frac{AN}{AB}\right)^{2}\cdot S_{\triangle ABC}=S\cos^{2}\alpha.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 109, с. 16
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 109, с. 14
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.2, с. 122
