61. AM
— биссектриса треугольника ABC
. Точка D
принадлежит стороне AC
, причём \angle DMC=\angle BAC
. Докажите, что BM=MD
.
Указание. Точки A
, B
, M
, D
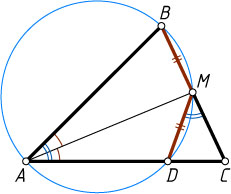
принадлежат одной окружности.
Решение. Поскольку
\angle BAC+\angle BMD=\angle DMC+\angle BMD=180^{\circ},
то точки A
, B
, M
, D
лежат на одной окружности, а так как \angle BAM=\angle MAD
, то BM=MD
(см. задачу 805).
Источник: Зубелевич Г. И. Сборник задач московских математических олимпиад. — 2-е изд. — М.: Просвещение, 1971. — № 419, с. 50
