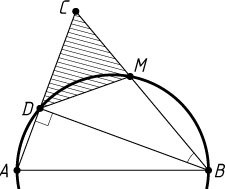
75. Отрезок AB
есть диаметр круга, а точка C
лежит вне этого круга. Отрезки AC
и BC
пересекаются с окружностью в точках D
и M
соответственно. Найдите угол CBD
, если площади треугольников DCM
и ACB
относятся как 1:4
.
Ответ. 30^{\circ}
.
Указание. Треугольник DCM
подобен треугольнику BCA
с коэффициентом \frac{1}{2}
(см. задачу 19).
Решение. Треугольники DCM
и BCA
подобны с коэффициентом \frac{1}{2}
(см. задачу 19), поэтому BC=2CD
. Следовательно,
\sin\angle CBD=\frac{CD}{BC}=\frac{1}{2},
а так как угол CBD
— острый, то \angle CBD=30^{\circ}
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1975, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 104
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 135, с. 17
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.4, с. 122
