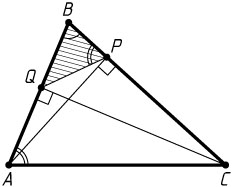
76. В остроугольном треугольнике ABC
из вершин A
и C
опущены высоты AP
и CQ
на стороны BC
и AB
. Известно, что площадь треугольника ABC
равна 18, площадь треугольника BPQ
равна 2, а PQ=2\sqrt{2}
. Найдите радиус окружности, описанной около треугольника ABC
.
Ответ. \frac{9}{2}
.
Указание. Треугольники BPQ
и BAC
подобны с коэффициентом \frac{1}{3}
(см. задачу 19).
Решение. Треугольники BPQ
и BAC
подобны по двум углам (см. задачу 19). Поскольку отношение их площадей равно \frac{2}{18}=\frac{1}{9}
, то коэффициент подобия равен \frac{1}{3}
. Значит, AC=3PQ=6\sqrt{2}
.
С другой стороны, коэффициент подобия равен \frac{BP}{AB}=\cos\angle B
. Поэтому \cos\angle B=\frac{1}{3}
. Тогда \sin\angle B=\frac{2\sqrt{2}}{3}
. Если R
— радиус описанной окружности треугольника ABC
, то
R=\frac{AC}{2\sin\angle B}=\frac{6\sqrt{2}}{2\cdot\frac{2\sqrt{2}}{3}}=\frac{9}{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1978, № 3, вариант 1
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 7
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 119
