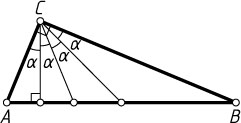
85. Известно, что в некотором треугольнике ABC
медиана, биссектриса и высота, проведённые из вершины C
, делят угол на четыре равные части. Найдите углы этого треугольника.
Ответ. 90^{\circ}
; 22{,}5^{\circ}
; 67{,}5^{\circ}
.
Указание. Докажите, что данный треугольник прямоугольный.
Решение. Обозначим каждый из этих углов через \alpha
. Если AC=BC
, то \alpha=0^{\circ}
, тогда \angle C=0^{\circ}
, что невозможно. Значит, AC\ne BC
. Поскольку биссектриса делит угол между высотой и медианой пополам и AC\ne BC
, то \angle C=90^{\circ}
(см. задачу 84), или 4\alpha=90^{\circ}
. Отсюда находим, что \alpha=22{,}5^{\circ}
. Следовательно острые углы треугольника равны 22{,}5^{\circ}
и 67{,}5^{\circ}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.66, с. 38
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.69, с. 38
