126. Формула Эйлера. Докажите, что O_{1}O^{2}_{2}=R^{2}-2rR
, где O_{1}
, O_{2}
— центры соответственно вписанной и описанной окружностей треугольника, r
, R
— радиусы этих окружностей.
Указание. Если B_{1}
— точка пересечения биссектрисы угла B
с описанной окружностью треугольника ABC
, то O_{1}B_{1}=B_{1}C
.
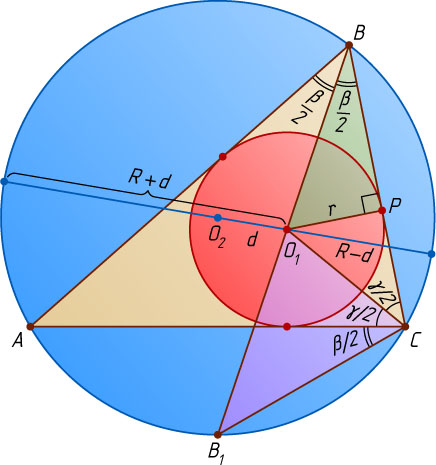
Решение. Первый способ. Пусть B_{1}
— точка пересечения биссектрисы треугольника ABC
, проведённой из вершины B
, с описанной окружностью (рис. 1). Обозначим \angle ABC=\beta
, \angle ACB=\gamma
. По теореме о внешнем угле треугольника
\angle B_{1}O_{1}C=\angle O_{1}BC+\angle O_{1}CB=\frac{\beta}{2}+\frac{\gamma}{2}.
С другой стороны,
\angle O_{1}CB_{1}=\angle O_{1}CA+\angle B_{1}CA=\angle O_{1}CA+\angle B_{1}BA=\frac{\gamma}{2}+\frac{\beta}{2}.
Значит, треугольник O_{1}B_{1}C
— равнобедренный. По теореме об отрезках пересекающихся хорд
B_{1}O_{1}\cdot O_{1}B=(R+O_{1}O_{2})(R-O_{1}O_{2})=R^{2}-O_{1}O^{2}_{2}.
Пусть P
— проекция точки O_{1}
на сторону BC
. Тогда O_{1}P=r
. Из прямоугольного треугольника BO_{1}P
находим, что
O_{1}B=\frac{O_{1}P}{\sin\angle O_{1}BP}=\frac{r}{\sin\frac{\beta}{2}},
а так как
B_{1}O_{1}=B_{1}C=2R\sin\angle B_{1}BC=2R\sin\frac{\beta}{2},
то
R^{2}-O_{1}O^{2}_{2}=\frac{r}{\sin\frac{\beta}{2}}\cdot2R\sin\frac{\beta}{2}=2rR.
Следовательно, O_{1}O^{2}_{2}=R^{2}-2rR
.
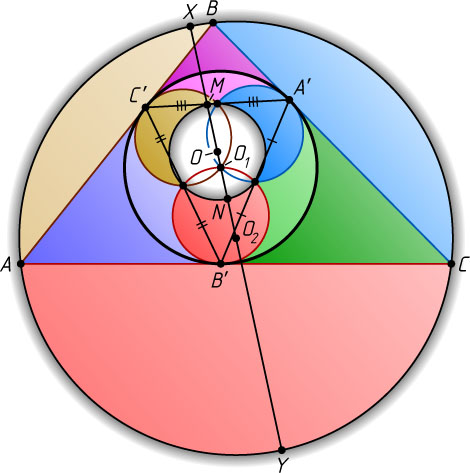
Второй способ. Пусть вписанная окружность касается сторон AB
, AC
и BC
треугольника ABC
в точках C'
, B'
и A'
соответственно (рис. 2). При инверсии относительно окружности с центром O_{1}
, вписанной в треугольник ABC
, вписанная окружность останется на месте, прямые, содержащие стороны треугольника перейдут в окружности, проходящие через центр O_{1}
инверсии и касающиеся окружности инверсии, поэтому вершины A
, B
и C
перейдут в середины отрезков B'C'
, A'C'
и B'C'
соответственно. Тогда окружность с центром O_{2}
, описанная около треугольника ABC
, перейдёт в окружность с центром O
радиуса \frac{r}{2}
, проходящую через середины сторон треугольника A'B'C'
. Эта окружность гомотетична описанной окружности треугольника ABC
, причём центр гомотетии совпадает с центром O_{1}
инверсии, значит, точка O
лежит на прямой O_{1}O_{2}
.
Пусть O_{1}O_{2}=d
, XY
— диаметр описанной окружности треугольника ABC
, проходящий через точку O_{1}
, а M
и N
— образы точек соответственно X
и Y
при рассматриваемой инверсии. Тогда
MN=XY\cdot\frac{r^{2}}{O_{1}X\cdot O_{1}Y}=2R\cdot\frac{r^{2}}{(R-d)(R+d)}=\frac{2Rr^{2}}{R^{2}-d^{2}},
а так как MN=r
, то \frac{2Rr^{2}}{R^{2}-d^{2}}=r
. Отсюда находим, что d^{2}=R^{2}-2rR
.
Третий способ. Обозначим
BC=a,~AC=b,~AB=c,~\angle BAC=\alpha,~\angle ABC=\beta,~\angle ACB=\gamma.
Предположим, что треугольник остроугольный. Тогда
\angle BOC=2\alpha,~\angle AOC=2\beta,~\angle AOB=2\gamma.
По теореме косинусов из треугольников BOC
, AOC
и AOB
находим, что
\cos2\alpha=\frac{2R^{2}-a^{2}}{2R^{2}}=1-\frac{a^{2}}{2R^{2}},~\cos2\beta=1-\frac{b^{2}}{2R^{2}},~\cos2\gamma=1-\frac{c^{2}}{2R^{2}}.
Если треугольник тупоугольный или прямоугольный, например, \alpha\geqslant90^{\circ}
, то \cos\angle BOC=\cos(360^{\circ}-2\alpha)=\cos2\alpha
, поэтому полученные формулы верны и в этом случае.
Пусть S
— площадь треугольника ABC
. Тогда S=\frac{abc}{4R}
и S=\frac{(a+b+c)r}{2}
. Поэтому \frac{abc}{4R}=\frac{(a+b+c)r}{2}
, откуда находим, что \frac{abc}{a+b+c}=2Rr
.
Воспользуемся формулой
\overrightarrow{O_{2}O_{1}}=\frac{a\overrightarrow{O_{2}A}+b\overrightarrow{O_{2}B}+c\overrightarrow{O_{2}C}}{a+b+c}.
Тогда
\overrightarrow{O_{2}O_{1}}^{2}=\left(\frac{a\overrightarrow{O_{2}A}+b\overrightarrow{O_{2}B}+c\overrightarrow{O_{2}C}}{a+b+c}\right)^{2}=
=\frac{1}{(a+b+c)^{2}}(a^{2}R^{2}+b^{2}R^{2}+c^{2}R^{2}+2abR^{2}\cos2\gamma+2acR^{2}\cos2\beta+2bcR^{2}\cos2\alpha)=
=\frac{R^{2}}{(a+b+c)^{2}}\left(a^{2}+b^{2}+c^{2}+2ab\left(1-\frac{c^{2}}{2R^{2}}\right)+2ac\left(1-\frac{b^{2}}{2R^{2}}\right)+2bc\left(1-\frac{a^{2}}{2R^{2}}\right)\right)=
=\frac{R^{2}}{(a+b+c)^{2}}\left((a+b+c)^{2}-\frac{abc^{2}}{R^{2}}-\frac{acb^{2}}{R^{2}}-\frac{bca^{2}}{R^{2}}\right)=
=\frac{R^{2}}{(a+b+c)^{2}}\left((a+b+c)^{2}-\frac{abc}{R}\cdot\frac{a+b+c}{R}\right)=R^{2}-\frac{abc}{a+b+c}=R^{2}-2Rr.
Что и требовалось доказать.
Примечание. 1. Из полученной формулы следует неравенство R\geqslant2r
, причём равенство достигается тогда и только тогда, когда треугольник равносторонний.
2. См. также статью И.Ф.Шарыгина «Вокруг биссектрисы», Квант, 1983, N8, с.32-36.
3. См. также статью В.Уроева «Инверсия», Квант, 1984, N5, с.26-32.
4. См. также статью В.Рыжика и Б.Сотниченко «Этюд о формуле Эйлера», Квант, 2007, N1, с.7-8.
5. Ещё один способ доказательства формулы Эйлера см. в примечании к задаче 13494.