13494. Угол при вершине C
треугольника ABC
равен 30^{\circ}
. Точки D
и E
лежат на сторонах AC
и BC
соответственно, причём AD=BE=AB
. Докажите, что OI=DE
и OI\perp DE
, где O
и I
— центры соответственно описанной и вписанной окружностей треугольника.
Решение. Решим более общую задачу. Обозначим \angle C=\gamma
, BC=a
, AC=b
, AB=c
(c\lt a
, c\lt b
), p
— полупериметр треугольника ABC
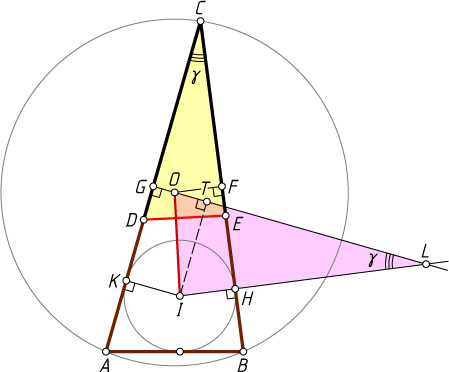
. Пусть F
и G
— проекции точки O
на прямые BC
и AC
соответственно, а H
и K
— проекции точки I
на прямые BC
и AC
соответственно. Тогда (см. задачу 219)
HF=BF-BH=\frac{a}{2}-(p-b)=\frac{b-c}{2}=\frac{AC-AB}{2}=\frac{AC-AD}{2}=\frac{1}{2}CD.
Аналогично, KG=\frac{1}{2}CE
.
Пусть продолжения отрезков GO
и IH
пересекаются в точке L
. Тогда \angle OLI=\angle C
(как углы с соответственно перпендикулярными сторонами), а если IT
— высота треугольника OLI
, то ITGK
— прямоугольник, поэтому TI=GK
. Значит,
LI=\frac{IT}{\sin\gamma}=\frac{GK}{\sin\gamma}=\frac{CE}{2\sin\gamma}.
Аналогично, LO=\frac{CD}{2\sin\gamma}
. Следовательно, треугольники LIO
и CED
подобны по двум сторонам и углу между ними. При этом LI\perp CE
и LO\perp CD
. Следовательно, IO\perp DE
. Кроме того,
IO=DE\cdot\frac{LI}{CE}=DE\cdot\frac{1}{2\sin\gamma}=\frac{DE}{2\sin\gamma},
а если \gamma=30^{\circ}
, то IO=DE
.
Примечание. 1. Доказательство рассмотренной более общей задачи см. в задаче 11713.
2. Из доказанного равенства IO=\frac{DE}{2\sin\gamma}
можно вывести формулу Эйлера (см. задачу 126). По теореме косинусов для треугольников CDE
и затем ABC
получаем:
IO^2=\left(\frac{DE}{2\sin\gamma}\right)^2=\frac{(a-c)^2+(b-c)^2-2(a-c)(b-c)\cos\gamma}{4\sin^2\gamma}=
=\frac{a^2+b^2-2ab\cos\gamma-2c(a+b-c)(1-\cos\gamma)}{4\sin^2\gamma}=
=\frac{c^2}{4\sin^2\gamma}-2\cdot\frac{c}{2\sin\gamma}\cdot(p-c)\frac{1-\cos\gamma}{\sin\gamma}=
=\left(\frac{c}{2\sin\gamma}\right)^2-2\cdot\frac{c}{2\sin\gamma}\cdot(p-c)\tg\frac{\gamma}{2}=R^2-2Rr.
Источник: Журнал «Crux Mathematicorum». — 1991, № 9, задача 3, с. 264
Источник: Китайские математические олимпиады. — 1988, первый отборочный этап
