128. Теорема Штейнера—Лемуса. Докажите, что если две биссектрисы треугольника равны, то он равнобедренный.
Указание. Докажите, что большему углу треугольника соответствует меньшая биссектриса.
Решение. Первый способ. Пусть \alpha
, \beta
, \gamma
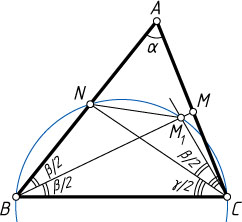
— углы при вершинах соответственно A
, B
и C
треугольника ABC
; BM
и CN
— биссектрисы треугольника. Предположим, что \beta\lt\gamma
.
Отложим от луча CN
в полуплоскости, содержащей точку M
, угол NCM_{1}
, равный \frac{\beta}{2}
, где M_{1}
— точка на биссектрисе BM
. Поскольку \frac{\beta}{2}\lt\frac{\gamma}{2}
, то точка M_{1}
лежит между точками B
и M
.
Отрезок NM_{1}
виден из точек B
и C
под одним углом, равным \frac{\beta}{2}
. Следовательно, точки B
, N
, M_{1}
и C
лежат на одной окружности, а BM_{1}
и CN
— хорды этой окружности. Поскольку
\angle BCM_{1}=\frac{\gamma}{2}+\frac{\beta}{2}\lt\frac{\alpha}{2}+\frac{\beta}{2}+\frac{\gamma}{2}=90^{\circ},
\angle BCM_{1}=\frac{\beta}{2}+\frac{\gamma}{2}\gt\beta=\angle NBC,
то хорда BM_{1}
видна из точки C
под острым углом, равным \frac{\gamma}{2}+\frac{\beta}{2}
, а хорда CN
видна из точки B
под острым углом, равным \beta
, причём \frac{\beta}{2}+\frac{\gamma}{2}\gt\beta
. Следовательно,
BM\gt BM_{1}\gt CN.
Таким образом, если углы треугольника не равны, то большему углу соответствует меньшая биссектриса. Следовательно, если биссектрисы равны, то равны и соответствующие им углы треугольника.
Второй способ. Пусть a
, b
и c
— стороны треугольника, \beta
и \gamma
— углы, противолежащие сторонам b
и c
соответственно, l_{b}
и l_{c}
— биссектрисы треугольника, проведённые из вершин этих углов. По известной формуле для площади треугольника имеем:
\frac{1}{2}ab\sin\gamma=\frac{1}{2}bl_{c}\sin\frac{\gamma}{2}+\frac{1}{2}al_{c}\sin\frac{\gamma}{2},
откуда находим, что
l_{c}=\frac{2ab\cos\frac{\gamma}{2}}{a+b}.
Аналогично
l_{b}=\frac{2ac\cos\frac{\beta}{2}}{a+c}.
Докажем, что если c\gt b
, то l_{c}\lt l_{b}
. В самом деле,
c\gt b~\Rightarrow~\gamma\gt\beta~\Rightarrow~\frac{\gamma}{2}\gt\frac{\beta}{2}~\Rightarrow~\cos\frac{\gamma}{2}\lt\cos\frac{\beta}{2};
c\gt b~\Rightarrow~a+c\gt a+b~\Rightarrow~\frac{1}{a+c}\lt\frac{1}{a+b}~\Rightarrow
\Rightarrow~\frac{a}{a+c}\lt\frac{a}{a+b}~\Rightarrow~1-\frac{a}{a+c}\gt1-\frac{a}{a+b}~\Rightarrow~\frac{c}{a+c}\gt\frac{b}{a+b}~\Rightarrow
\Rightarrow~\frac{ac}{a+c}\gt\frac{ab}{a+b}~\Rightarrow~l_{c}=\frac{2ac\cos\frac{\beta}{2}}{a+c}\gt\frac{2ab\cos\frac{\gamma}{2}}{a+b}=l_{b}.
Таким образом, если стороны треугольника не равны, то к большей стороне проведена меньшая биссектриса. Следовательно, если биссектрисы равны, то равны и соответствующие им стороны треугольника.
Третий способ. Выразим квадраты обеих биссектрис через стороны треугольника (см. задачу 4751) и приравняем полученные выражения. Пусть p=\frac{a+b+c}{2}
. Тогда
l_{c}^{2}=\frac{4p(p-c)ab}{(a+b)^{2}}=\frac{ab(a+b+c)(a+b-c)}{(a+b)^{2}},
l_{b}^{2}=\frac{4p(p-b)ac}{(a+c)^{2}}=\frac{ac(a+b+c)(a+c-b)}{(a+c)^{2}},
\frac{ab(a+b+c)(a+b-c)}{(a+b)^{2}}=\frac{ac(a+b+c)(a+c-b)}{(a+c)^{2}}~\Leftrightarrow
\Leftrightarrow~b(a+b-c)(a+c)^{2}=c(a+c-b)(a+b)^{2}~\Leftrightarrow
\Leftrightarrow~b^{3}c-bc^{3}+3abc(b-c)+a^{2}(b^{2}-c^{2})+a^{3}(b-c)=0~\Leftrightarrow
\Leftrightarrow~(b-c)(b^{2}c+bc^{2}+a^{2}b+ac^{2}+a^{3}+3abc)=0.
Выражение, стоящее во второй скобке, положительно, поэтому b=c
.
Примечание. См. также статью А.Коробова: «Семь решений задачи Штейнера», Квант, 1996, N4, с.38-40 и статью З.Дегтярёвой и Д.Максимова: «Снова теорема Штейнера-Лемуса», Квант, 2021, N2, с.37-40.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 96, с. 31
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 74, с. 187; № 138, с. 193
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 23
Источник: Тригг Ч. Задачи с изюминкой. — М.: Мир, 1975. — с. 24, № 61
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 335
Источник: Дынкин Е. Б. и др. Математические задачи. — М.: Наука, 1966. — № 37, с. 12
Источник: Журнал «Crux Mathematicorum». — 1977, № 6, с. 148
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 499(а), с. 60
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 31
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 24, с. 6
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.55, с. 107
Источник: Журнал «Квант». — 1996, № 4, с. 38-40
