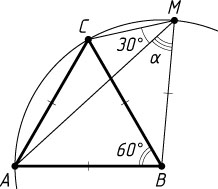
135. Вне правильного треугольника ABC
, но внутри угла BAC
взята точка M
так, что угол CMA
равен 30^{\circ}
и угол BMA
равен \alpha
. Найдите угол ABM
.
Ответ. 180^{\circ}-2\alpha
.
Указание. Проведите окружность в центром в точке B
и радиусом BA
. Точка M
принадлежит этой окружности.
Решение. С центром в точке B
и радиусом BA
проведём окружность. Тогда точка M
принадлежит этой окружности (см. задачу 2900). Значит, треугольник ABM
— равнобедренный. Следовательно,
\angle ABM=180^{\circ}-2\angle AMB=180^{\circ}-2\alpha.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.111, с. 42
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.32, с. 105
