137. В круге проведены два перпендикулярных диаметра AE
и BF
. На дуге EF
взята точка C
. Хорды CA
и CB
пересекают диаметры BF
и AE
в точках P
и Q
соответственно. Докажите, что площадь четырёхугольника APQB
равна квадрату радиуса круга.
Указание. \angle CAE+\angle CBF=45^{\circ}
,
\tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\tg\beta}
.
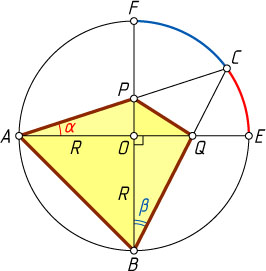
Решение. Пусть O
— центр круга, R
— радиус. Обозначим \angle CAE=\alpha
, \angle CBF=\beta
. Поскольку \alpha+\beta=45^{\circ}
, то
\tg(\alpha+\beta)=\tg45^{\circ}=1,
а так как
\tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\tg\beta}
то
\tg\alpha+\tg\beta=1-\tg\alpha\tg\beta.
Площадь четырёхугольника с перпендикулярными диагоналями равна половине произведения диагоналей (см. задачу 3018), значит,
S_{APQB}=\frac{1}{2}AQ\cdot BP=\frac{1}{2}(AO+OQ)(BO+OP)=
=\frac{1}{2}(R+R\tg\alpha)(R+R\tg\beta)=\frac{R^{2}}{2}(1+\tg\alpha)(1+\tg\beta)=
=\frac{R^{2}}{2}(1+\tg\alpha+\tg\beta+\tg\alpha\tg\beta)=
=\frac{R^{2}}{2}(1+1-\tg\alpha\tg\beta+\tg\alpha\tg\beta)=R^{2}.
