167. Точка E
лежит на стороне AC
правильного треугольника ABC
; точка K
— середина отрезка AE
. Прямая, проходящая через точку E
перпендикулярно прямой AB
, и прямая, проходящая через точку C
перпендикулярно прямой BC
, пересекаются в точке D
. Найдите углы треугольника BKD
.
Ответ. 90^{\circ}
, 30^{\circ}
, 60^{\circ}
.
Указание. Пусть F
— проекция точки E
на AB
. Докажите, что точки K
, F
, B
, C
и D
лежат на одной окружности.
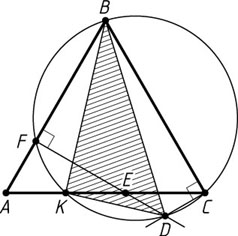
Решение. Пусть F
— основание перпендикуляра, опущенного из точки E
на AB
. Тогда FK
— медиана прямоугольного треугольника AFE
. Поэтому \angle AKF=60^{\circ}
и FK\parallel BC
(см. задачу 1109).
Опишем окружность около равнобедренной трапеции BFKC
. Точка D
принадлежит этой окружности, так как \angle BFD+\angle BCD=180^{\circ}
; BD
— диаметр этой окружности, так как \angle BCD=90^{\circ}
. Следовательно,
\angle BKD=90^{\circ},~\angle BDK=\angle BCK=60^{\circ},~\angle KBD=30^{\circ}.
Источник: Вступительный экзамен в МФТИ. — 1976, билет 12, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 76-12-4, с. 190
Источник: Журнал «Квант». — 1979, № 9, с. 40, задача 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.22, с. 12
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 24, с. 140
