171. Докажите, что если для вписанного четырёхугольника ABCD
выполнено равенство CD=AD+BC
, то биссектрисы его углов A
и B
пересекаются на стороне CD
.
Указание. Пусть M
и P
— точки на основании CD
такие, что CP=BC
, а AM
— биссектриса угла BAD
. Тогда точки A
, M
, P
и B
лежат на одной окружности.
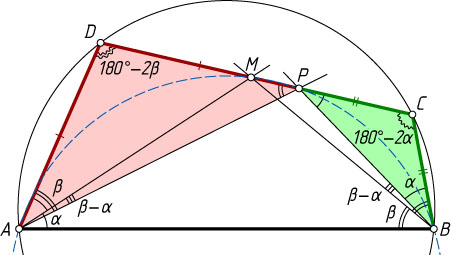
Решение. Обозначим \angle A=2\alpha
, \angle B=2\beta
. Предположим, что \alpha\lt\beta
. Отложим на отрезке CD
отрезок CP
, равный BC
. Тогда DP=AD
, треугольники BCP
и APD
— равнобедренные,
\angle D=180^{\circ}-2\beta,~\angle PAD=\angle DPA=\beta,
\angle C=180^{\circ}-2\alpha,~\angle CBP=\angle CPB=\alpha.
Пусть AM
— биссектриса угла BAD
(M
на стороне CD
). Поскольку \angle MAD=\alpha\lt\beta=\angle PAD
, то точка M
лежит между точками P
и D
,
\angle PMA=180^{\circ}-2\beta+\alpha,~\angle PBA=2\beta-\alpha.
Поэтому
\angle PMA+\angle PBA=180^{\circ}.
Тогда точки P
, M
, A
, B
лежат на одной окружности. Значит,
\angle PBM=\angle PAM=\beta-\alpha.
Следовательно,
\angle CBM=\angle CBP+\angle PBM=\alpha+\beta-\alpha=\beta=\frac{1}{2}\angle CBA,
т. е. BM
— биссектриса угла CBA
.
Примечание. Верно и обратное: если биссектрисы углов при вершинах A
и B
вписанного четырёхугольника ABCD
пересекаются на стороне CD
, то CD=AD+BC
(см. задачу 262).