262. Докажите, что если биссектрисы углов при вершинах A
и B
вписанного четырёхугольника ABCD
пересекаются на стороне CD
, то CD=AD+BC
.
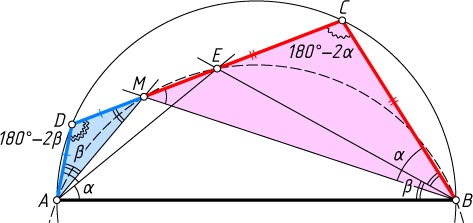
Решение. Первый способ. Пусть \angle A=2\alpha
, \angle B=2\beta
, \alpha\gt\beta
, а биссектрисы углов A
и B
пересекаются в точке E
, лежащей на стороне CD
.
От луча AD
в полуплоскость, содержащую точку E
, отложим луч под углом \beta
. Поскольку \beta\lt\alpha
, этот луч проходит между сторонами угла DAE
, поэтому он пересекает сторону CD
в некоторой точке M
, лежащей между D
и E
,
\angle AMD=180^{\circ}-\angle DAM-\angle ADC=180^{\circ}-\angle DAM-(180^{\circ}-\angle ABC)=
=180^{\circ}-\beta-(180^{\circ}-2\beta)=\beta.
Поэтому треугольник ADM
— равнобедренный, AD=DM
, а \angle AMC=180^{\circ}-\beta
. Значит, точки A
, M
, E
и B
лежат на одной окружности. Тогда
\angle BMC=\angle BME=\angle BAE=\alpha,
\angle CBM=180^{\circ}-\angle BCM-\angle MBC=180^{\circ}-(180^{\circ}-2\alpha)-\alpha=\alpha,
поэтому треугольник BMC
— также равнобедренный, BC=MC
. Следовательно,
AD+BC=DM+MC=DC.
Второй способ. Достаточно доказать, что если окружность с центром на стороне CD
касается сторон AD
, AB
и BC
вписанного четырёхугольника ABCD
, то CD=AD+BC
.
Пусть P
и Q
— точки касания этой окружности со сторонами AD
и BC
соответственно, r
— радиус окружности, \angle ADC=\delta
, \angle BCD=\gamma
.
Луч AO
— биссектриса угла BAD
, поэтому
\angle OAP=\frac{1}{2}\angle BAD=\frac{1}{2}(180^{\circ}-\angle BCD)=90^{\circ}-\frac{\gamma}{2},
значит, \angle AOP=\frac{\gamma}{2}
. Тогда
AP=OP\tg\angle AOP=r\tg\frac{\gamma}{2}.
Аналогично, BQ=r\tg\frac{\delta}{2}
.
Из прямоугольных треугольников DOP
, COQ
, AOP
и BOQ
находим, что
PD=r\ctg\delta,~OD=\frac{r}{\sin\delta},~CQ=r\ctg\gamma,~OC=\frac{r}{\sin\gamma},
AP=r\tg\frac{\gamma}{2},~BQ=r\tg\frac{\delta}{2}.
Следовательно,
AD+BC=(AP+PD)+(BQ+CQ)=
=\left(r\tg\frac{\gamma}{2}+r\ctg\delta\right)+\left(r\tg\frac{\delta}{2}+r\ctg\gamma\right)=
=r\left(\tg\frac{\gamma}{2}+\ctg\gamma\right)+r\left(\tg\frac{\delta}{2}+\ctg\delta\right)=
=r\left(\frac{\sin\frac{\gamma}{2}\sin\gamma+\cos\frac{\gamma}{2}\cos\gamma}{\cos\frac{\gamma}{2}\sin\gamma}+\frac{\sin\frac{\delta}{2}\sin\delta+\cos\frac{\delta}{2}\cos\delta}{\cos\frac{\delta}{2}\sin\delta}\right)=
=r\left(\frac{\cos\frac{\gamma}{2}}{\cos\frac{\gamma}{2}\sin\gamma}+\frac{\cos\frac{\delta}{2}}{\cos\frac{\delta}{2}\sin\delta}\right)=r\left(\frac{1}{\sin\gamma}+\frac{1}{\sin\delta}\right)=
=\left(\frac{r}{\sin\gamma}+\frac{r}{\sin\delta}\right)=OC+OD.
Что и требовалось доказать.
Примечание. Верно и обратное: если ABCD
— вписанный четырёхугольник и CD=AD+BC
, то биссектрисы углов при вершинах A
и B
пересекаются на стороне CD
(см. задачу 171).
Источник: Всероссийская олимпиада школьников. — 1974-75, I, IV этап, 10 класс
